Сетевой график: пример построения

Основные определения

Ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг, называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в направлении достижения результата при осуществлении комплекса работ.Наиболее распространен способ представления моделируемого комплекса работ в понятиях работ и событий.Понятие «работа» имеет следующие значения:

• «действительная работа» – процесс, требующий затрат времени и ресурсов;
• «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.

Работа на графике изображается стрелкой, над которой указывается затрачиваемое на нее время. Длина стрелки и ее ориентация на графике не имеют значения. Желательно только выдерживать направление стрелок так, чтобы начальное событие для работы (обозначается i) располагалось слева в сетевом графике, а конечное (обозначается j) — справа. Для отображения фиктивных работ используют пунктирные стрелки, над которыми время не указывается или проставляется ноль.

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 1. Каждая операция в сети представляется одной и только одной дугой (стрелкой). Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой.

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?б) Какие операции должны непосредственно следовать после завершения данной операции?в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелказавершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Предварительный этап построения сетевого графика

На предварительном этапе сетевого планирования необходимо определить характер планируемых операций и потенциал сотрудников, которые будут отвечать за их выполнение.

В качестве примера возьмем работу регионального Агентства по молодежной политике на месяц и запланируем перечень операций на месяц.

Допустим, что количество сотрудников – 10 человек.

Типовая оргструктура Агентства по молодежной политике

Построение сетевого графика представляет собой элемент управленческой деятельности и соответствует общему процессу принятия решений. Это неотъемлемая составляющая процесса управления. В ходе построения сетевого графика рассматриваются несколько вариантов выполнения запланированных операций и в итоге выбирается наилучшая альтернатива из множества доступных. В сетевой график включаются непосредственно управленческие действия и операции, связанные с технической стороной деятельности организации.

Управленческие и технические операции в сетевом графике

Управленческие операции	Технические операции
Общее управление внутренними процессами в организации	Непосредственное проведение запланированных операций
Проектирование системы управления	Подведение итогов
Стратегическое планирование	Работа с документами, регистрами
Управленческое консультирование	Оценка результатов
Управление сотрудниками	Оформление документации
Взаимодействие с внешней средой	Формализация результатов

Операции в сетевом графике должны быть зафиксированы документально, например, в распорядительных документах. Основное назначение такой документации состоит в регулировании деятельности объекта управления, обеспечении его финансовыми, трудовыми, материальными и информационными ресурсами. Основные формы документального представления запланированных операций:

1. Приказы – в том числе распоряжения, указания;
2. Акты – в том числе акцепты и протоколы;
3. Договоры – в том числе, соглашения, контракты, оферты;
4. Регламенты – инструкции, положения, правила, планы, модели.

Работа с расписанием в МКП

Этапы алгоритма МКП с 1-го по 3-й достаточно подробно изложены в статье на тему практики построения сетевого графика. Ниже мною приведен пример фрагмента модели, на которой критический путь показан стрелочками красного цвета. Его определить достаточно просто. Двигаться следует от конечной работы к начальной. Необходимо выбирать из всех предыдущих действий операцию, имеющую самое позднее раннее окончание. Именно такие операции будут лежать на критическом пути. Его нахождение можно выполнить и в табличной форме, пример применения МКП также приведен в указанном выше материале.

Пример фрагмента сетевого графика с выделенным критическим путем

В практике оптимизации календарных моделей действуют два иногда конкурирующих между собой ориентира: критический путь и загруженность временных ресурсов. На стыке интересов сохранения или уменьшения общего срока, с одной стороны, и достаточности ресурсов, с другой, строится деятельность по моделированию календаря. Среди способов действий в зоне взаимодействия данных интересов выделяются два: сглаживание ресурсов и их выравнивание.

Первый метод позволяет выполнить анализ и оптимизировать ресурсы, не заходя за рамки имеющихся резервов на выполнение задач мероприятия, и критический путь остается неизменным. При выравнивании РМ получает возможность изменения сроков работ, включая и операции критического пути. Это приводит к изменению сроков всего проекта. Все зависит от доминирования того или иного критерия среди сроков и ресурсного обеспечения. Ниже на схеме приведен перечень методов, которые руководитель может использовать для оптимизации модели.

Способы оптимизации модели календарного планирования

При проведении ресурсной оптимизации следует руководствоваться несколькими правилами:

• итерационно обращаться к методологии по мере надобности в течение всего периода реализации инвестиционного мероприятия;
• каждое действие следует наделять ресурсом с учетом его стоимости;
• не допускать длительной перегрузки ресурсов;
• учитывать уровень дискретности выполнения операций;
• выполнять анализ доступности ресурсов на основе календарей их загрузки;
• для выравнивания ресурсов использовать матрицу приоритета задач.

Что РМ может предпринять, если он не укладывается в установленные ему свыше сроки выполнения основной задачи, при этом ресурсные резервы еще не исчерпаны? Менеджер может выполнить сжатие календарного плана путем интенсификации работ, их распараллеливания или использовать комбинированный метод. Интенсификация применяется к работам, находящимся на критическом пути. Операции планируется выполнить быстрее, но при этом возрастает риск увеличения их стоимости за счет ресурсного насыщения. Второй способ предполагает сдвиг последующей операции на более ранние сроки, что дает эффект общего сокращения работ за счет параллельного выполнения. При этом возникает опасность, что работу придется переделывать.

МКП входит в состав базовых компетенций современного руководителя. Обладая видением критических задач, PM способен принимать более взвешенные решения по возможностям изменения графика, урезания несущественных действий и оптимизации ресурсов. Процедуры эти в рамках процессов планирования носят итеративный характер и позволяют построить оптимизированное, но вполне реалистичное расписание проекта.

Построение сетевого графика

В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.

В таблицу сведем следующие данные по каждой операции:

• номер операции;
• предшествующие операции;
• количество исполнителей;
• продолжительность операции в днях.

В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.

Таблица операций для построения сетевого графика

Номер операции	Предыдущие операции	Кол-во исполнителей, чел.	Продолжительность, дни
1.	—	10	1
2.	1	2	3
3.	1	3	1
4.	1	2	4
5.	4	1	0,5
6.	3	3	2
7.	5	2	0,5
8.	2,7,6	10	0,5
9.	9	10	0,5
10.	9	1	3
11.	9	2	4
12.	9	2	2
13.	9	2	3
14.	12	2	2
15.	13	3	2
16.	10,11,14,15	10	0,5
17.	16	10	0,5
18.	17	2	2
19.	18	2	3
20.	17	2	2
21.	17	2	3
22.	21	3	1
23.	20	2	2
24.	19,22,23	10	0,5
25.	24	10	0,5
26.	25	5	1
27.	26	5	3
28.	25	3	2
29.	28	3	2
30.	25	2	4
31.	27,29,30	10	0,5
32.	31	10	0,5
33.	32	7	1
34.	32	2	1
35.	33,34	10	1

На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.

Сетевой график, пример

Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.

В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.

Для соблюдения запланированных сроков произведем корректировку сетевого графика.

В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.

После корректировки осуществим построение альтернативного сетевого графика.

Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:

Q = N * t

Q4 = 2*4 = 8 ч/дн

Q13 = 2*3 = 6 ч/дн

Q18 = 2*2 = 4 ч/дн

В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.

В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.

В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.

В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:

26 – 2 – 1 – 1 = 22 дня.

Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.

Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.

Альтернативный сетевой график

Основные разделы сетевой схемы Smartdraw

Это главный экран, с которым мы будем работать, чтобы создать нашу схему сети.

Мы собираемся начать говорить о разделах, которые у вас есть, отмечая красными квадратами, начиная сверху вниз. Вверху, где находится «Файл», о котором я говорил ранее, находится «Главное меню». Вот некоторые из возможных вариантов:

• Вставить : чтобы вставить изображение, ссылку или объект.
• Настольные : поставить стол, если он нам нужен.
• Поддержка : если нам нужна помощь.

Во второй области слева у нас есть типичные стрелки для продвижения и задержки действий на случай, если мы допустили ошибку или хотим увидеть, подходит ли нам больше сейчас или раньше. Другие интересные кнопки:

• Форма : для рисования геометрических фигур, таких как круги, прямоугольники и т. д. Если вы хотите, вы можете добавить текст внутри.
• линия (слева): сделать разные типы линий для подключения устройств.
• Текст : добавить текст.
• линия (справа): чтобы раскрасить линии.
• эффекты : используется для установки эффектов на некоторые объекты. Например, установите тень на прямоугольник.

Третий раздел Компьютеры и серверы где находятся значки, которые мы можем использовать для создания нашей сети. Просто двойным щелчком выбранный символ появится в нашей рабочей области. Если мы нажмем на значок работы, он будет заключен в квадрат с четырьмя стрелками направления.

В случае вытягивания одной из 4-х стрелок рядом с нами создастся другая идентичная команда. например, вот что произошло бы, если бы мы потянули стрелку вправо.

Четвертый раздел под значками, которые мы можем использовать, содержит ряд стрелок и имеет поведение, очень похожее на то, что я только что объяснил. Например, если мы нажмем на Добавить право, выбранная нами команда будет размещена справа.

Наконец, пятая часть будет работать аналогичным образом. В этом случае я бы добавил еще два в команду, из которой он стартует в указанном направлении, чтобы в итоге сформировать набор из трех (они не обязательно должны быть одинаковыми).

При табличном методе расчета параметров сетевой модели ранние начала работ, выходящих из исходного события, принимаются равными нулю, остальные работы рассчитываются по формуле:

, (3)

где t_ро(n-1) — ранние окончания предшествующих работ.

Раннее окончание работы:

, (4)

где t_n – продолжительность n–ой работы.

Позднее начало работы:

. (5)

Поздние окончания работ, входящих в завершающее событие, принимаются равными максимальному раннему окончанию завершающего события, остальные работы рассчитываются по формуле:

, (6)

где t_пн(n+1) – поздние начала последующих работ.

Полный резерв времени:

(7)

или

. (8)

Резерв времени второго вида определяется для событий, которые являются конечным событием нескольких работ:

, (9)

где t_ро(n)i – ранние окончания работ, приходящих в одно событие.

Таким образом, методы сетевого планирования и управления обеспечивают руководителей и исполнителей на всех участках работы обоснованной информацией, которая необходима им для принятия решений по планированию, организации и управлению.

Выводы

Методы сетевого планирования и управления обеспечивают руководителей и исполнителей на всех участках работы обоснованной информацией, которая необходима им для принятия решений по планированию, организации и управлению. А при использовании вычислительной техники сетевое планирование и управление является уже не просто одним из методов планирования, а автоматизированным методом управления производственным процессом.

Линейный график, хотя и довольно нагляден, но не в состоянии отразить сложность моделируемого процесса, установить взаимосвязь отдельных технологических процессов, выявить решающие участки работ, выдать необходимые прогнозы по состоянию работ.

Отличительными особенностями сетевых графиков являются:

– наличие взаимосвязей между работами и технологической последовательностью их исполнения;

– возможность выявления работ, от завершения которых в первую очередь зависит продолжительность строительства;

– возможность выбора вариантов последовательности и продолжительности работ с целью улучшения сетевого графика;

– облегчение контроля за ходом строительства;

– возможность использования ЭВМ для расчётов параметров графика при планировании и управлении.

Основные элементы, используемые для сетевого графика

Построение графиков начинается с обозначения теоретических основ. Рассмотрим основные элементы, требующиеся для составления модели:

1. Любое событие обозначается кружком, в середине которого находится цифра, соответствующая порядку действий.
2. Сама работа – это стрелка, ведущая от одного события к другому. Над стрелкой пишут время, необходимое для ее совершения, а под стрелкой обозначают ответственное лицо.

Работа может выполниться в трех состояниях:

— Действующая – это обыкновенное действие, на совершение которого требуются затраты времени и ресурсов.

— Ожидание – процесс, во время которого ничего не происходит, но он требует затрат времени для перехода от одного события к другому.

— Фиктивная работа – это логическая связь между событиями. Она не требует ни времени, ни ресурсов, но чтобы не прервать сетевой график, ее обозначают пунктирной линией. Например, подготовка зерна и приготовление мешков для него — это два отдельных процесса, они не связаны последовательно, но их связь нужна для следующего события – фасовки. Поэтому выделяют еще один кружочек, который соединяют пунктиром.

Минимизация числа исполнителей проекта при сохранении времени его выполнения

линейная диаграммакарта проекта

• минимизировать количество одновременно занятых исполнителей;
• выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.

• перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
• работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
• работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
• перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
• передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.

калькулятора

Таблица 1

Работа (ij)	Длительность t(ij), дн.	Количество исполнителей
1,2	4	5
2,3	6	3
2,4	5	6
2,7	11	6
3,5	9	1
4,6	9	2
5,7	11	3
6,7	10	5
7,8	4	6

Рис. 1. Пример сетевого графика

Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.

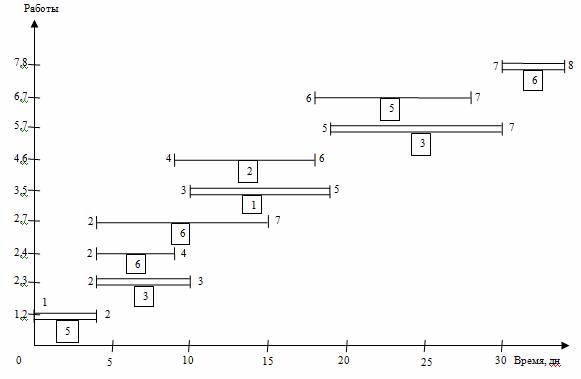
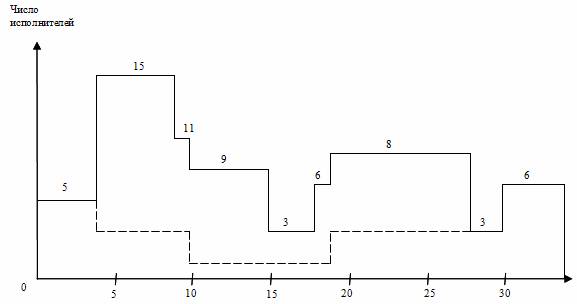Рис. 2. Линейная диаграмма и карта проекта до оптимизации

15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.

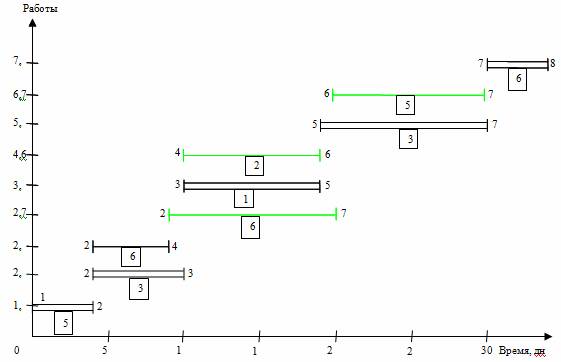
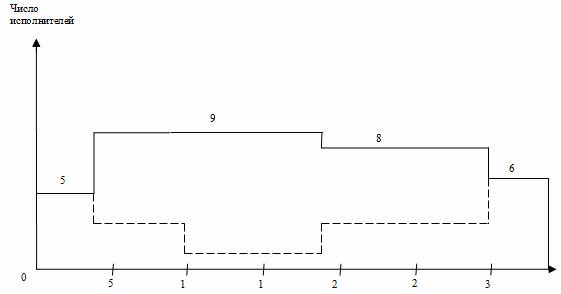
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено.

Видеоинструкция

Алгоритм построения сетевого графика

Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.

Шаг 1. Определить основную цель проекта

Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.

Шаг 2. Выявить ограничения

Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.

Шаг 4. Оценить длительность работ

Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.

Шаг 5. Определить последовательность работ

Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.

Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.

Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.

Шаг 6. Указать связи между работами

Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.

Шаг 7. Определить раннее начало и раннее окончание

Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.

Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.

Шаг 8. Определить поздние начало и окончание

Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Шаг 9. Определить временной резерв

Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Шаг 10. Выявить критический путь

Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.

Заключение

В современных условиях производственно-хозяйственной деятельности от руководителей любого уровня требуется: научная деятельность планирования, оперативность в управлении и проведении контроля за ходом работ, своевременное и гибкое реагирование на часто изменяющуюся обстановку, умелое маневрирование резервами в зависимости от важности и первоочередности работ. В таких условиях одного опыта и таланта руководителя явно недостаточно, так как уже недостаточно иметь тщательно составленный календарный график, опытных исполнителей

Возникла необходимость в новом методе планирования и управления, который отвечал бы следующим основным требованиям и позволял: координировать деятельность всех исполнителей; оценивать обоснованность сроков выполнения работ; совершенствовать планирование и материально-техническое снабжение; обоснованно прогнозировать выполнение планируемых работ; своевременно принимать меры к предупреждению возможных срывов; правильно определять потребные материальные и людские ресурсы для реализации плана; концентрировать внимание руководителей на наиболее важных участках, которые определяют длительность всей работы; применять вычислительную технику в управлении. Перечисленным требованиям отвечает система сетевого планирования и управления, позволяющая на основе сетевого и: структурного графика планировать и управлять производственно-хозяйственной деятельностью

Методы сетевого планирования и управления обеспечивают руководителей и исполнителей на всех участках работы обоснованной информацией, которая необходима им для принятия решений по планированию, организации и управлению. А при использовании вычислительной техники сетевое планирование и управление является уже не просто одним из методов планирования, а автоматизированным методом управления производственным процессом.

Линейный график, хотя и довольно нагляден, но не в состоянии отразить сложность моделируемого процесса, установить взаимосвязь отдельных технологических процессов, выявить решающие участки работ, выдать необходимые прогнозы по состоянию работ.

Отличительными особенностями сетевых графиков являются:

– наличие взаимосвязей между работами и технологической последовательностью их исполнения;

– возможность выявления работ, от завершения которых в первую очередь зависит продолжительность строительства;

– возможность выбора вариантов последовательности и продолжительности работ с целью улучшения сетевого графика;

– облегчение контроля за ходом строительства;

– возможность использования ЭВМ для расчётов параметров графика при планировании и управлении.

В практической части работы построен график работ по внедрению новой производственной линии в ООО «ХСМ».

В результате расчетов сетевого графика подготовки производства усовершенствованного изделия и его оптимизации удалось достичь равномерного распределения ресурса на протяжение всего периода подготовки производства (5 человек). Период внедрения проекта, в свою очередь, не выходит за пределы директивного (заданного) срока и составляет 23 дня, что на один день меньше изначально рассчитанного.