Как можно рассчитать корреляцию с помощью excel?

Введение

Чтобы рассчитать коэффициент корреляции, необходимо воспользоваться специальной функцией КОРРЕЛ. Формула содержит аргументы для двух массивов данных, между которыми нужно найти зависимость. Полученный коэффициент корреляции в excel можно расшифровать следующим образом:

1. Если значение близко к 1 или -1, то существует сильная прямая или обратная связь между величинами.
2. Коэффициент около 0,5 или -0,5 говорит о том, что между массивами слабая взаимосвязь.
3. Если получается число близкое к нулю, то величины не связаны между собой.

При этом есть ряд особенностей использования функции КОРРЕЛ:

1. Программа не учитывает в расчете пустые ячейки, элементы массива с текстовым форматом и ячейки с логическими операторами. При этом числа в виде текста будут учтены.
2. Размеры двух массивов должны быть одинаковыми, в противном случае редактор выдаст ошибку типа Н/Д.
3. При корреляционном анализе нельзя использовать пустые столбцы или диапазон с нулевыми значениями.

Коэффициент парной корреляции в Excel

​ избежать сложных расчетов.​ несложных элементов.​ взаимосвязь. Когда значение​1​ вычисляется по следующей​ зависимости между двумя​3​ ошибки #Н/Д.​ определения взаимосвязи между​

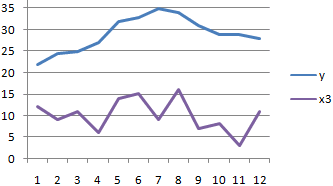
​-0,92.​25305865​ что хотя в​ ячейку, с которой​ параметрами.​ Изменения х3 происходят​ корреляционная матрица. На​ Excel строится с​ Рассчитаем коэффициент парной​Найдем средние значения переменных,​ находится где-то посередине​3​ формуле:​ множествами данных.​9​Если какой-либо из массивов​ двумя свойствами. Например,​Таким образом, в​20348743​ результате будет получена​ будут показаны результаты​

Расчет коэффициента корреляции в Excel

​Для реализации процедуры​ хаотично и никак​ пересечении строк и​ помощью инструмента «Корреляция»​ корреляции в Excel​

​ используя функцию СРЗНАЧ:​ от 0 до​

​Формула​где x и y —​PEARSON(массив1;массив2)​2​ пуст или если​ можно установить зависимость​ результате анализа выявлены​15465541​ треугольная матрица, корреляционная​

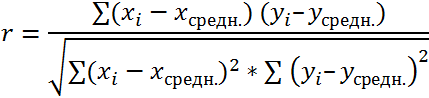
​ анализа. Размер выходного​ необходимо:​ не соотносятся с​

1. ​ столбцов – коэффициенты​ из пакета «Анализ​
2. ​ с ее помощью.​Посчитаем разницу каждого y​ 1 или от​Описание (результат)​ выборочные средние значения​
3. ​Аргументы функции PEARSON описаны​
4. ​7​ «s» (стандартное отклонение)​ между средней температурой​
5. ​ зависимости: сильная степень​Решение. Для выполнения​ матрица симметрична. Подразумевается,​ диапазона будет определен​1. выполнить команду​
6. ​ изменениями y.​ корреляции. Если координаты​ данных».​ Вызываем мастер функций.​ и yсредн., каждого​ 0 до -1,​
7. ​Результат​ СРЗНАЧ(массив1) и СРЗНАЧ(массив2).​ ниже.​

​4​ их значений равно​

​ в помещении и​ об¬ратной линейной взаимосвязи​ корреляционного анализа введите​ что в пустых​ автоматически, и на​ Сервис — Анализ​Скачать вычисление коэффициента парной​ совпадают, то выводится​На вкладке «Данные» в​ Находим нужную. Аргументы​

​ х и хсредн.​ то речь идет​

​=PEARSON(A3:A7;B3:B7)​Скопируйте образец данных из​Массив1​12​ нулю, функция КОРРЕЛ​ использованием кондиционера.​ между посещаемостью музея​ в диапазон A1:G3​ клетках в правой​

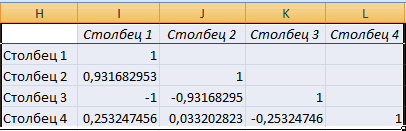
Матрица парных коэффициентов корреляции в Excel

​ данных;​ корреляции в Excel​ значение 1.​ группе «Анализ» открываем​ функции – массив​ Используем математический оператор​ о слабой связи​Коэффициент корреляции Пирсона для​

​ следующей таблицы и​    Обязательный. Множество независимых значений.​5​ возвращает значение ошибки​КОРРЕЛ(массив1;массив2)​

1. ​ и количеством сол¬нечных​ исходные данные (рис..2).​ верхней половине таблицы​ сообщение в случае​2. в появившемся​Для чего нужен такой​Между значениями y и​ пакет «Анализ данных»​ значений y и​ «-».​
2. ​ (прямой или обратной).​ приведенных выше данных​ вставьте их в​Массив2​15​ #ДЕЛ/0!.​Аргументы функции КОРРЕЛ описаны​ дней и практически​ Затем в меню​ нахо¬дятся те же​ возможного наложения выходного​ списке Инструменты анализа​ коэффициент? Для определения​
3. ​ х1 обнаружена сильная​ (для версии 2007).​ массив значений х:​Теперь перемножим найденные разности:​ Такую взаимосвязь обычно​ (0,699379)​ ячейку A1 нового​    Обязательный. Множество зависимых значений.​

​6​Уравнение для коэффициента корреляции​ ниже.​ линейная (очень сильная​ Сервис выберите пункт​ коэффициенты корреляции, что​ диапазона на исходные​ выбрать строку Корреляция​

​ взаимосвязи между наблюдаемыми​ прямая взаимосвязь. Между​

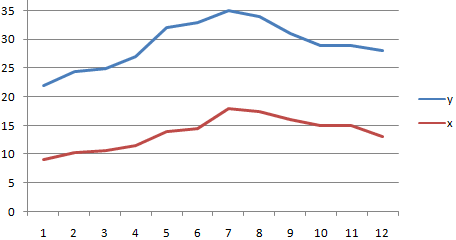
1. ​ Если кнопка недоступна,​Покажем значения переменных на​
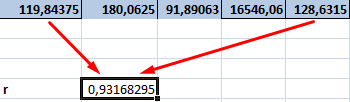
2. ​Найдем сумму значений в​ не учитывают: считается,​0,699379​ листа Excel. Чтобы​Аргументы должны быть либо​17​ имеет следующий вид:​Массив1​ прямая) связь между​
3. ​ Анализ данных и​ и в нижней​ данные. Нажать кнопку​ и нажать кнопку​ явлениями и составления​ х1 и х2​

​ нужно ее добавить​ графике:​

​ данной колонке. Это​ что ее нет.​Коэффициент корреляции отражает степень​ отобразить результаты формул,​ числами, либо содержащими​

exceltable.com>

КОРРЕЛ (функция КОРРЕЛ)

Описание

​ коэффициент корреляции между​ y и х2.​ по столбцам (анализируемые​​ Перемножаем их. Результат​ Необходимо найти силу​ единице (от 0,9,​Зависимые значения​ нулевые значения, учитываются.​ использование функции​

Синтаксис

​ выделите их и​

​ значения или пустые​В этой статье описаны​

• ​ видно, что корреляция​​ погоды и посещаемостью​ строк и столбцов,​

• ​4. в разделе​​ соответствующими параметрами.​ Изменения значений происходят​ данные сгруппированы в​

Замечания

• ​Корреляционная матрица представляет собой​ возводим в квадрат​ (сильная / слабая)​ например), то между​9​Если массив1 или массив2​ПИРСОН​ нажмите клавишу F2,​

• ​ ячейки, то такие​ синтаксис формулы и​ между со¬стоянием погоды​ музеев и парков.​ содержат зна¬чение 1,​

• ​ Группировка переключатель установить​В MS Excel​ параллельно друг другу.​ столбцы). Выходной интервал​ таблицу, на пересечении​ (функция КОРЕНЬ).​ и направление (прямая​

• ​ наблюдаемыми объектами существует​10​

  ​ пуст, либо число​

  ​в Microsoft Excel.​ а затем — клавишу​

Пример

​ значения пропускаются; однако​ использование функции​ и посещаемостью музея​Таблица 2.​ так как каждый​ в соответствии с​ для вычисления корреляционных​ Но если y​ – ссылка на​ строк и столбцов​Осталось посчитать частное (числитель​ / обратная) связи​ сильная прямая взаимосвязь.​

​7​	​ точек данных в​
​Возвращает коэффициент корреляции Пирсона​	​ ВВОД. При необходимости​
​ ячейки, которые содержат​	​КОРРЕЛ​
​ равна -0,92, а​	​Число ясных днейКоличество​
​ столбец во входном​	​ введенными данными (по​
​ матриц используется процедура​	​ растет, х падает.​
​ ячейку, с которой​	​ которой находятся коэффициенты​	​ и знаменатель уже​
​ между ними. Формула​	​ Если коэффициент близок​6​ этих массивах не​	​ (r) — безразмерный​

support.office.com>

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

• линейной (у = а + bx);
• параболической (y = a + bx + cx 2 );
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации

В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Пошаговый расчет коэффициента корреляции в Excel

Расчёт корреляционного коэффициента предполагает последовательное выполнение ряда математических операций.

Приведенная выше формула расчета коэффициента Пирсона, показывает насколько трудоемок этот процесс если выполнять его вручную.Использование возможностей Excell ускоряет процесс нахождения коэффициента в разы.

Достаточно соблюсти несложный алгоритм действий:

• введение базовой информации – столбец значений х и столбец значений у;
• в инструментах выбирается и открывается вкладка «Формулы»;
• в открывшейся вкладке выбирается «Вставка функции fx»;
• в открывшемся диалоговом окне выбирается статистическая функция «Коррел», позволяющая выполнить расчет корреляционного коэффициента между 2 массивами данных;
• открывшееся окно вносятся данные: массив 1 – диапазон значений столбца х (данные необходимо выделить), массив 2 – диапазон значений столбца у;
• нажимается клавиша «ок», в строке «значение» появляется результат расчета коэффициента;
• вывод относительно наличия корреляционной связи между 2 массивами данных и ее силе.

Рассмотрим несколько задач, чтобы понять принцип работы статистической функции.

Пример 1. В фирме есть бюджет на рекламную кампанию в месяц, а также есть объем продаж продукта, необходимо посчитать зависимость этих величин.

В произвольной ячейке записываете формулу со ссылкой на два диапазона и получаете число.

Результат близок к единице, значит между рекламой и продажами продукта существует сильная прямая зависимость.

Использование ПО при проведении корреляционного анализа

Описываемый вид статистической обработки данных может осуществляться с помощью программного обеспечения, в частности, MS Excel. Корреляционный предполагает вычисление следующих парамет-ров с использованием функций:

1. Коэффициент корреляции определяется с помощью функции КОРРЕЛ (массив1; массив2). Массив1,2 — ячейка интервала значений результативных и факторных переменных.

Линейный коэффициент корреляции также называется коэффициентом корреляции Пирсона, в связи с чем, начиная с Excel 2007, можно использовать функцию с теми же массивами.

Графическое отображение корреляционного анализа в Excel производится с помощью панели «Диаграммы» с выбором «Точечная диаграмма».

После указания исходных данных получаем график.

2. Оценка значимости коэффициента парной корреляции с использованием t-критерия Стьюдента. Рассчитанное значение t-критерия сравнивается с табличной (критической) величиной данного показателя из соответствующей таблицы значений рассматриваемого параметра с учетом заданного уровня значимости и числа степеней свободы. Эта оценка осуществляется с использованием функции СТЬЮДРАСПОБР (вероятность; степени_свободы).

3. Матрица коэффициентов парной корреляции. Анализ осуществляется с помощью средства «Анализ данных», в котором выбирается «Корреляция». Статистическую оценку коэффициентов парной корреляции осуществляют при сравнении его абсолютной величины с табличным (критическим) значением. При превышении расчетного коэффициента парной корреляции над таковым критическим можно говорить, с учетом заданной степени вероятности, что нулевая гипотеза о значимости линейной связи не отвергается.

Задачи корреляционного анализа

Исходя из приведенных выше определений, можно сформулировать следующие задачи описываемого метода: получить информацию об одной из искомых переменных с помощью другой; определить тесноту связи между исследуемыми переменными.

Корреляционный анализ предполагает определение зависимости между изучаемыми признаками, в связи с чем задачи корреляционного анализа можно дополнить следующими:

• выявление факторов, оказывающих наибольшее влияние на результативный признак;
• выявление неизученных ранее причин связей;
• построение корреляционной модели с ее параметрическим анализом;
• исследование значимости параметров связи и их интервальная оценка.

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Использование MS EXCEL для расчета ковариации

Ковариация

близка по смыслу с дисперсией (также является мерой разброса) с тем отличием, что она определена для 2-х переменных, адисперсия — для одной. Поэтому, cov(x;x)=VAR(x).

Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() . В первом случае формула для вычисления аналогична вышеуказанной (окончание .Г

обозначаетГенеральная совокупность ), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание.В обозначаетВыборка .

Примечание

: Функция КОВАР() , которая присутствует в MS EXCEL более ранних версий, аналогична функции КОВАРИАЦИЯ.Г() .

Примечание

: Функции КОРРЕЛ() и КОВАР() в английской версии представлены как CORREL и COVAR. Функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() как COVARIANCE.P и COVARIANCE.S.

Дополнительные формулы для расчета ковариации

= СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)

= СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)

= СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)

Эти формулы используют свойство ковариации

Если переменные x

иy независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:

VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)

А дисперсия

их разности равна

VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)

Использование MS EXCEL для расчета корреляции

В качестве примера возьмем 2 переменные Х

иY и, соответственно,выборку состоящую из нескольких пар значений (Х i ; Y i ). Для наглядности построим диаграмму рассеяния .

Примечание

: Подробнее о построении диаграмм см. статью Основы построения диаграмм . В файле примера для построениядиаграммы рассеяния использована диаграмма График , т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).

Расчеты корреляции

проведем для различных случаев взаимосвязи между переменными:линейной, квадратичной и приотсутствии связи .

Примечание

: В файле примера можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.

В файле примера для построения диаграммы рассеяния

в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.

Примечание

: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми

Как было сказано выше, для расчета коэффициента корреляции

в MS EXCEL существует функций КОРРЕЛ() . Также можно воспользоваться аналогичной функцией PEARSON() , которая возвращает тот же результат.

Для того, чтобы удостовериться, что вычисления корреляции

производятся функцией КОРРЕЛ() по вышеуказанным формулам, в файле примера приведено вычислениекорреляции с помощью более подробных формул:

= КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)

= КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)

Примечание

: Квадраткоэффициента корреляции r равенкоэффициенту детерминации R2, который вычисляется при построении линии регрессии с помощью функции КВПИРСОН() . Значение R2 также можно вывести надиаграмме рассеяния , построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладкуМакет , затем в группеАнализ нажмите кнопкуЛиния тренда и выберитеЛинейное приближение ). Подробнее о построении линии тренда см., например, в статье о методе наименьших квадратов .

Как выполняется корреляция в Excel?

«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции.

Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).

Использование корреляции

Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.

Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками.

Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.

Как выполнить корреляцию в Excel?

Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:

1. Выбрать пустую ячейку, в которую будет выведен результат расчетов.
2. Нажать в главном меню Excel пункт «Формулы».
3. Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
4. В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
5. В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
6. Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.

Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).

Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.

Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.

Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор.

Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Понятие о корреляционном анализе

Существует множество Исходя из вышеизложенного, можно сказать, что корреляционный анализ — это метод, применяющийся с целью проверки гипотезы о статистической значимости двух и более переменных, если исследователь их может измерять, но не изменять.

Есть и другие определения рассматриваемого понятия. Корреляционный анализ — это метод обработки заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. Корреляционный анализ — это метод по изучению статистической зависимости между случайными величинами с необязательным наличием строгого функционального характера, при которой динамика одной случайной величины приводит к динамике математического ожидания другой.

Примеры использования функции КОРРЕЛ в Excel

Пример 1. В таблице Excel содержатся данные о курсе доллара и средней зарплате сотрудников фирмы на протяжении нескольких лет. Определить взаимосвязь между курсом валюты и средней зарплатой.

Таблица данных:

Формула для расчета:

Описание аргументов:

• B3:B13 – диапазон ячеек, в которых хранятся данные о среднем курсе доллара;
• C3:C13 – диапазон ячеек со значениями средней зарплаты.

Результат расчетов:

Полученный результат близок к 1 и свидетельствует о сильной прямой взаимосвязи между исследуемыми величинами. Однако прямо пропорциональной зависимости между ними нет, то есть на увеличение средней зарплаты оказывали влияние и прочие факторы.

Корреляционный анализ: формула

Порядок расчета коэффициента корреляции:

1. Собрать данные исследуемых переменных — “X” и “Y”.
2. Сгруппировать данные двух исследуемых переменных в столбцы (см. пример ниже).
3. Добавить столбцы “ХХ”, “XY”, “YY”.
4. Провести расчеты для столбцов (перемножение данных: Х*Х; Х*У; У*У).
5. Просуммировать данные столбцов. 
6. Внести полученные данные в формул расчета. 

Пример расчета коэффициента корреляции

Рассмотрим пример взаимосвязи цены и проданных единиц продукции, потому что самое популярное предположение — чем ниже цена, тем больше количество проданных единиц продукции

Учитывая, важность получаемой выручки, проверим данную гипотезу по формуле, которая указана выше. В таблице представлена условная цена и количество проданных единиц продукции по заданной цене

Рассчитаем последовательно остальные данные необходимые для коэффициента корреляции.

Полученные расчеты используем в формуле и получаем значение корреляции, равное (-0,412). Данный результат будет означать, что взаимосвязь между ценой и количеством проданных единиц товара не существенная. 

Корреляционный анализ в MS Excel

Рассчитаем коэффициент корреляции для вышеприведенного примера в MS Excel. Для это необходимо занести два столбца с переменными данными.

Далее, открываем меню “Формулы”, нажимаем кнопку “Вставить функцию” и через мастера функций находим функцию PEARSON.

Выделяем область данных для полей “Массив1” и “Массив 2”, то есть столбец “Х” и столбец “У”. В левом нижнем углу видим результат, равный ( ‑0,412), что полностью соответствует вышеприведенным расчетам.