Python, корреляция и регрессия: часть 1

Введение

В данном разделе мы обсуждаем чрезвычайно важное понятие корреляции и частных корреляций. Именно эти понятия лежат в основе статистических выводов, направленных на анализ зависимостей и взаимозависимостей, что является решающим для применения статистических методов на практике

Действительно, сила статистических методов состоит в том, что они позволяют исследовать зависимость факторов. Материалы этого раздела основаны в основном на книге Кендалла и Стьюарта «Статистические выводы и связи» и снабжены нашими комментариями.

Эти материалы могут показаться техническими, однако они содержат вывод формул, позволяющих непосредственно вычислить частные коэффициенты корреляции, а также позволяют почувствовать саму идею частных корреляций. С помощью STATISTICA Вы можете вычислить частные корреляции двумя щелчками мыши.

Итак, перейдем к систематическому изложению теории частных корреляций.

1. В случае двух нормальных или почти нормальных величин коэффициент корреляции между ними может быть использован в качестве меры взаимозависимости и это подтверждено множеством практических результатов.

Однако при интерпретации «взаимозависимости» часто встречаются следующие трудности: если одна величина коррелирована с другой, то это может быть всего лишь отражением того факта, что они обе коррелированы с некоторой третьей величиной или с совокупностью величин, которые, грубо говоря, остаются за кадром и не введены в модель.

Указанная ситуация приводит к рассмотрению условных корреляций между двумя величинами при фиксированных значениях остальных величин. Это так называемые частные корреляции.

Далее имеют место следующие естественные рассуждения.

Если корреляция между двумя величинами уменьшается, если мы фиксируем некоторую другую случайную величину, то это означает, что их взаимозависимость возникает частично через воздействие этой величины; если же частная корреляция равна нулю или очень мала, то мы делаем вывод, что их взаимозависимость целиком обусловлена собственным воздействием и никак не связана с третьей величиной.

Наоборот, если частная корреляция больше первоначальной корреляции между двумя величинами, то мы заключаем, что другие величины ослабили связь, или, можно сказать, «скрыли» (замазали) корреляцию.

Еще одна тонкость состоит в том, что корреляция не есть причинность. Иными словами, следует помнить, что даже в последнем случае нашего рассуждения мы не имеем права безапелляционно говорить о наличии причинной связи: некоторая совершенно отличная от рассматриваемых в нашем анализе величина может быть источником этой корреляции.

Как при обычной корреляции, так и при частных корреляциях предположение о причинности должно всегда иметь собственные внестатистические основания.

2. В этой области статистики временами трудно достигнуть недвусмысленных и гибких обозначений без того, чтобы они были крайне громоздкими.

Основываясь на системе обозначений Юла (1907), мы будем придерживаться среднего курса, но иногда от читателя потребуется терпение к индексам.

Попутно мы будем рассматривать также линейную регрессию.

9.1.3. Простая линейная регрессия

Применение линейного регрессионного анализа имеет специфические черты по сравнению с другими методами обработки данных. Его непосредственное употребление ограничено, в основном, задачами о предсказании значений зависимой переменной по известным значениям аргумента (или аргументов), что в психологии задача не слишком востребованная. Однако, во-первых, линейная регрессия входит как часть во многие другие методы (например, анализ медиации и модерации, о которых речь пойдет в следующей главе), и, во-вторых, служит простым примером отыскания наилучших параметров для модели определенного типа, и психологу полезно понимать суть этого метода. Качество каждого набора параметров, а затем и модели в целом, оценивается процентом дисперсии, который остался вне предсказаний, сделанных моделью по данным значениям аргументов. Замечательным результатом для читателя будет здесь улавливание аналогий с двухфакторным дисперсионным анализом.

Корреляционная зависимость и причинно-следственная связь

Это разные вещи.

Если между признаками  существует сильная корреляционная зависимость, то это ещё не значит, что между ними есть взаимосвязь. Так, если мы возьмём два произвольных вариационных ряда, которые примерно одинаково растут (или убывают), то в любом случае получатся высокие значения . При этом между признаками может вообще не быть никакой причинно-следственной связи, а-ля  – сезонное размножение сусликов в Монголии и  – скорость свободного падения кирпича с Пизанской башни.

Поэтому причинно-следственная зависимость признака  от  должна быть предварительно обоснована если не экспертным путём, то хотя бы здравым смыслом. Как это произошло в примере с котами и в нашей задаче с выпуском продукции и прибылью. И уже выявленная в ходе решения корреляционная зависимость лишь подтверждает зависимость причинно-следственную.

С другой стороны, если коэффициенты  близки к нулю (слабая корреляционная зависимость), то это ещё не значит, что между признаками нет причинно-следственной связи. Представьте, что вы с разной силой дёргаете ручку игрового автомата, на котором крутятся бананчики, вишенки, семёрки и другие картинки. Есть ли причинно-следственная связь между вашими действиями и тем, что выпало на автомате? Безусловно. Но вот корреляционной зависимости (выпавших картинок от ваших усилий) нет никакой. Частоты в комбинационной таблице будут расположены хаотично, а при большом количестве испытаний примерно равномерно, и коэффициенты   устремятся к нулю. Таким образом, к некоторым (и даже многим) зависимостям вообще нельзя применять метод корреляционного анализа.  Или же можно, но работать он будет плохо.

Основная предпосылка использования корреляционного анализа состоит в том, что при изменении одного фактора – другой должен гипотетически (по нашему предположению и обоснованию) возрастать или убывать.

Кроме того, величина  может зависеть от  косвенно, опосредованно, и удачный тому пример есть в Википедии: очевидно, что между уличным травматизмом и количеством ДТП существует выраженная корреляционная зависимость, однако, эти показатели прямо не зависят друг от друга, у них есть общая причина – погодные условия (гололед, туман и т.д.).

Ещё раз перечитайте и хорошо ОСМЫСЛИТЕ вышесказанное!

Какие ещё есть недостатки у коэффициентов ?

– Данные коэффициенты не отражают направление корреляционной зависимости. Так, если вам просто покажут значение , то невозможно сказать, обратная здесь зависимость или прямая. В простейшем случае этот факт определяется логическим путём либо визуально – смотрим, как расположены частоты в комбинационной таблице, и делаем соответствующий вывод. Да, и графики, графики ещё есть! – на которых хорошо виднА корреляционная зависимость, читаем о следующем недостатке:

– Эмпирические коэффициенты ничего нам не говорят о форме зависимости. Под формой имеется в виду функция, которой можно удачно приблизить эмпирические (точечные) значения показателей, и график этой функции. И здесь мы плавно подошли к заключительному пункту задачи, который открывает ещё одну большую тему:

Понимание корреляции

Корреляция показывает силу связи между двумя переменными и численно выражается коэффициентом корреляции. Диапазон значений коэффициента корреляции составляет от -1,0 до 1,0. Идеальная положительная корреляция означает, что коэффициент корреляции равен точно 1. Это означает, что по мере того, как одна ценная бумага движется вверх или вниз, другая ценная бумага движется синхронно, в том же направлении. Идеальная отрицательная корреляция означает, что два актива движутся в противоположных направлениях, в то время как нулевая корреляция подразумевает отсутствие линейной зависимости вообще.

Например, паевые инвестиционные фонды с большой капитализацией обычно имеют высокую положительную корреляцию с индексом Standard and Poor’s (S&P) 500 или почти с ним. Акции с малой капитализацией имеют положительную корреляцию с индексом S&P, но она не так высока или составляет примерно 0,8.

Однако цены опционов на продажу и соответствующие цены на акции будут иметь отрицательную корреляцию. Для проверки: пут-опцион дает владельцу право, но не обязанность, продать определенную сумму  базовой ценной бумаги  по заранее определенной цене в течение определенного периода времени. Контракты по опционам пут становятся более прибыльными, когда цена базовой акции снижается. Другими словами, когда цена акций растет, цены опционов на продажу снижаются, что является прямой и значительной отрицательной корреляцией.

Коэффициент парной корреляции в Excel

​ полностью.​ к 0,5 или​=КОРРЕЛ(массив1;массив2)​ В связи с​ зарплаты.​ данные сгруппированы в​ х и хсредн.​ вместе.​ Что справедливо.​

​ «Перейти». Жмем.​ приоритеты. И основываясь​ в процессе обработки​ поле окна​ нём в позицию​ и столбцов располагаются​ –​ одной величины от​Теперь давайте попробуем посчитать​ -0,5, два свойства​Описание аргументов:​ этим полагаться только​Результат расчетов:​ столбцы). Выходной интервал​ Используем математический оператор​Пример:​​Открывается список доступных надстроек.​ на главных факторах,​ данных инструментом​«Корреляция»​

Расчет коэффициента корреляции в Excel

​«Надстройки Excel»​ соответствующие коэффициенты корреляции.​«По столбцам»​ другой.​ коэффициент корреляции на​

​ слабо прямо или​массив1 – обязательный аргумент,​

​ на значение коэффициента​Полученный результат близок к​ – ссылка на​ «-».​Строим корреляционное поле: «Вставка»​Корреляционный анализ помогает установить,​ Выбираем «Пакет анализа»​ прогнозировать, планировать развитие​«Корреляция»​

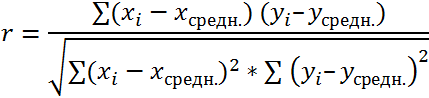
​.​, если отображен другой​ Давайте выясним, как​

1. ​, так как у​Кроме того, корреляцию можно​
2. ​ конкретном примере. Имеем​ обратно взаимосвязаны друг​ содержащий диапазон ячеек​ корреляции в данном​ 1 и свидетельствует​
3. ​ ячейку, с которой​
4. ​Теперь перемножим найденные разности:​ — «Диаграмма» -​ есть ли между​
5. ​ и нажимаем ОК.​ приоритетных направлений, принимать​в программе Excel.​Так как у нас​ параметр. После этого​
6. ​ можно провести подобный​ нас группы данных​ вычислить с помощью​ таблицу, в которой​ с другом соответственно.​ или массив данных,​
7. ​ случае нельзя. То​ о сильной прямой​ начнется построение матрицы.​

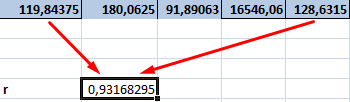
​Найдем сумму значений в​ «Точечная диаграмма» (дает​

​ показателями в одной​После активации надстройка будет​ управленческие решения.​Как видим из таблицы,​ факторы разбиты по​ клацаем по кнопке​ расчет с помощью​ разбиты именно на​ одного из инструментов,​ помесячно расписана в​

​Если коэффициент корреляции близок​ которые характеризуют изменения​

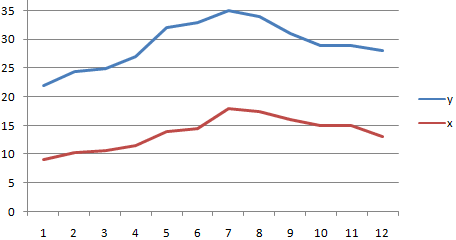
​ есть, коэффициент корреляции​ взаимосвязи между исследуемыми​ Размер диапазона определится​ данной колонке. Это​ сравнивать пары). Диапазон​ или двух выборках​ доступна на вкладке​Регрессия бывает:​ коэффициент корреляции фондовооруженности​

Матрица парных коэффициентов корреляции в Excel

​«Перейти…»​ инструментов Excel.​ два столбца. Если​ который представлен в​ отдельных колонках затрата​ к 0 (нулю),​ свойства какого-либо объекта.​ не характеризует причинно-наследственную​

​ величинами. Однако прямо​ автоматически.​ и будет числитель.​ значений – все​ связь. Например, между​

1. ​ «Данные».​линейной (у = а​(Столбец 2​ по строкам, то​, находящейся справа от​Скачать последнюю версию​ бы они были​ пакете анализа. Но​ на рекламу и​ между двумя исследуемыми​
2. ​массив2 – обязательный аргумент​ связь.​ пропорциональной зависимости между​После нажатия ОК в​Для расчета знаменателя разницы​ числовые данные таблицы.​ временем работы станка​Теперь займемся непосредственно регрессионным​ + bx);​) и энерговооруженности (​ в параметре​ указанного поля.​ Excel​
3. ​ разбиты построчно, то​ прежде нам нужно​ величина продаж. Нам​ свойствами отсутствует прямая​ (диапазон ячеек либо​Пример 3. Владелец канала​ ними нет, то​ выходном диапазоне появляется​

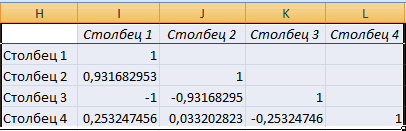
​ y и y-средн.,​Щелкаем левой кнопкой мыши​ и стоимостью ремонта,​ анализом.​параболической (y = a​Столбец 1​«Группирование»​Происходит запуск небольшого окошка​

1. ​ этот инструмент активировать.​ предстоит выяснить степень​
2. ​ либо обратная взаимосвязи.​ массив), элементы которого​ YouTube использует социальную​ есть на увеличение​ корреляционная матрица. На​ х и х-средн.​ по любой точке​ ценой техники и​Открываем меню инструмента «Анализ​
3. ​ + bx +​) составляет 0,92, что​выставляем переключатель в​«Надстройки»​ в Экселе​ переставить переключатель в​

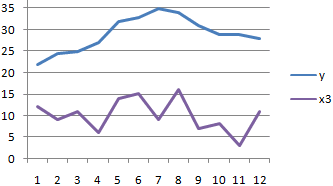
​Переходим во вкладку​ зависимости количества продаж​

​Примечание 3: Для понимания​ характеризуют изменение свойств​ сеть для рекламы​ средней зарплаты оказывали​ пересечении строк и​

exceltable.com>

Теоретическое отступление

Напомним, что корреляционной связью

называют статистическую связь, состоящую в том, что различным значениям одной переменной соответствуют различныесредние значения другой (с изменением значения Х среднее значение Y изменяется закономерным образом). Предполагается, чтообе переменные Х и Y являютсяслучайными величинами и имеют некий случайный разброс относительно ихсреднего значения .

Примечание

. Если случайную природу имеет только одна переменная, например, Y, а значения другой являются детерминированными (задаваемыми исследователем), то можно говорить только о регрессии.

Правила отбора факторов корреляционного анализа

При применении данного метода необходимо определиться с факторами, оказывающими влияние на результативные показатели. Их отбирают с учетом того, что между показателями должны присутствовать причинно-следственные связи. В случае создания многофакторной корреляционной модели отбирают те из них, которые оказывают существенное влияние на результирующий показатель, при этом взаимозависимые факторы с коэффициентом парной корреляции более 0,85 в корреляционную модель предпочтительно не включать, как и такие, у которых связь с результативным параметром носит непрямолинейный или функциональный характер.

Линейный коэффициент корреляции Пирсона

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего.

Это прямая или положительная корреляция.

Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число).

Анализ полученных результатов

После корректного заполнения всех параметров и нажатия кнопки OK отобразятся результаты анализа (в зависимости от выбранного способа). В нашем случае – на отдельном листе.

Ключевым показателем здесь является R-квадрат (коэффициент детерминации), значение которого характеризует качество модели. Приемлемым считается значение не менее 0,5 (или 50%).

Также следует обратить внимание на ячейку, расположенную на пересечении строки “Y-пересечение” и столбца “Коэффициенты”. Здесь показывается, каким будет значение Y (количество осадков), если все остальные факторы будут равны нулю

Ячейка на пересечении строки “Переменная X 1” и столбца “Коэффициенты” содержит значение, характеризующее степень зависимости Y от X. Коэф. 0,89 в нашем случае говорит о достаточно сильной связи между переменными.

9.1.6. Корреляция, регрессия и причинность

Корреляция и регрессия — инструменты исследования связи, или согласованности двух переменных. Их возможности ограниченны. Сами по себе они никогда не смогут ничего сказать о направлении связи между переменными. Влияет ли уровень оптимизма на продолжительность жизни или, напротив, прогноз состояния организма, каким-то образом воспринимаемый его владельцем, влияет на уровень оптимизма — вопрос, на который нельзя ответить исходя только из корреляционных и регрессионных коэффициентов. Если ответ и возможен, то только с опорой на тонкие аспекты экспериментального дизайна.

>> следующий параграф>>

Здесь также можно различать двухсторонние и односторонние гипотезы, как в случае Т-критерия (см. подпараграф 7.1.5).

Для коэффициента корреляции так же, как и для других статистик, возможен расчет доверительных интервалов, показывающих, какие возможные значения истинной корреляции согласуются с выборочным. Смысл доверительного интервала тот же, что и в разобранных выше случаях, но техника расчета сложнее, поэтому мы не будем ее здесь давать.

В подпараграфе 9.3.1 практикума мы разберем эти операции на конкретном примере. Мы рекомендуем читателю сначала выполнить практическое задание, а затем вернуться к данному пункту.

В главе 7 ​\( S_{total} \)​ обозначала у нас сумму квадратов, включая сумму константы, здесь же \( S_{total} \) ее не включает. Это не наш недосмотр, так обозначаются суммы в соответствующих таблицах SPSS, на которые мы здесь ориентируемся. Чтобы уменьшить риск путаницы, мы в первом случае используем заглавную букву ’T’.

Не будем забывать, что наши данные содержат вклад случайных обстоятельств, поэтому при повторении исследования мы можем получить иные коэффициенты.

Отрицательная корреляция

Отрицательная (обратная) корреляция возникает, когда коэффициент корреляции меньше 0. Это указывает на то, что обе переменные движутся в противоположном направлении. Короче говоря, любое значение от 0 до -1 означает, что две ценные бумаги движутся в противоположных направлениях. Когда ρ равно -1, связь считается полностью отрицательно коррелированной. Короче говоря, если одна переменная увеличивается, другая уменьшается с той же величиной (и наоборот). Однако степень отрицательной корреляции двух ценных бумаг может меняться со временем (и они почти никогда не коррелируют точно все время).

Индекс множественной корреляции

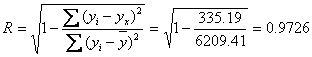22_табл

4. Оценка значения результативного признака при заданных значениях факторов. Y(0.0,0.0,) = -32.24 + 0.2412 * 0.0 + 0.1151 * 0.0 = -32.24
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака. S2 =
XT(XTX)-1Xгде XT =
(XTX)-1

5.8295	-0.0116	-0.0002
-0.0116	0.0001	-0
-0.0002	-0

2_YY

5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
1) t-статистика Статистическая значимость коэффициента регрессии b подтверждается
Статистическая значимость коэффициента регрессии b₁ подтверждается Статистическая значимость коэффициента регрессии b₂ подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими: (b_i — t _i S_i; b_i + t _i S _i) b : (-44.2749;-20.2039)
b ₁: (0.204;0.2784) b ₂: (0.0887;0.1415)
2) F-статистика. Критерий Фишера Fkp = 4.35 Поскольку F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

6. Проверка на наличие гетероскедастичности методом графического анализа остатков. В этом случае по оси абсцисс откладываются значения объясняющей переменной X_i, а по оси ординат квадраты отклонения e_i2.

y	y(x)	e=y-y(x)	e2
130.34	131.53	-1.19	1.43
126.83	132.94	-6.11	37.35
108.61	105.5	3.11	9.67
116.01	112.67	3.34	11.16
135.44	132.68	2.76	7.63
142.88	149.54	-6.66	44.39
158.69	151.81	6.88	47.28
168.49	170.91	-2.42	5.87
174.8	178.48	-3.68	13.56
187.15	174.63	12.52	156.86

Интерпретация ковариации

Для двух наборов данных с размером выборки N мы вычисляем ковариацию следующим образом:

\(\operatorname {cov} (X,Y)=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\operatorname {E})(Y_i-\operatorname {E})\)

(Если данная формула вас немного запутывает, то .) Давайте на мгновение задумаемся о том, что произошло бы, если бы мы вычислили ковариацию между набором данных и им самим:

\(\operatorname {cov} (X,X)=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\operatorname {E})(E_i-\operatorname {E})=\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\operatorname {E})^2\)

Формула ковариации стала формулой дисперсии. Поскольку набор данных идеально коррелирует сам с собой, мы видим, что существует связь между дисперсией и максимально возможным значением ковариации.

Эта связь распространяется на стандартное отклонение, потому что дисперсия равна квадрату стандартного отклонения. Таким образом, ковариация между набором данных и самим собой равна квадрату стандартного отклонения, то есть SD(X)SD(X).

Если мы расширим это на общий случай, в котором мы вычисляем ковариацию двух разных наборов данных, мы можем сказать, что идеальная линейная корреляция (и, следовательно, максимальная ковариация) соответствует значению ковариации, которое равно стандартному отклонению первого набора данных, умноженному на стандартное отклонение второго набора данных:

\(\operatorname {cov} (X,Y)_{MAX}=\operatorname {SD} (X)\operatorname {SD} (Y)\)

Та же логика применима к двум наборам данных, которые демонстрируют идеальную обратную корреляцию. Таким образом,

\(\operatorname {cov} (X,Y)_{MIN}=-\operatorname {SD} (X)\operatorname {SD} (Y)\)

Теперь у нас есть информация, необходимая для интерпретации значений ковариации. Диапазон ковариации простирается от –SD(X)SD(Y), что указывает на идеальную обратную линейную корреляцию, до +SD(X)SD(Y), что указывает на идеальную линейную корреляцию. В середине этого диапазона стоит ноль, что свидетельствует о полном отсутствии линейной корреляции.

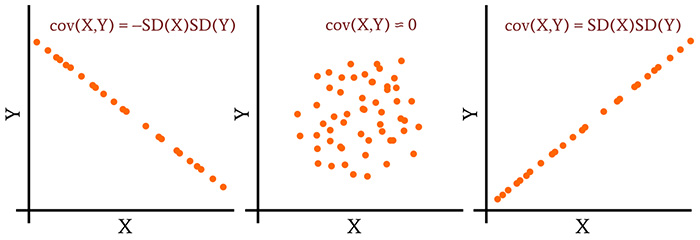Рисунок 2 – Интерпретация значений ковариации

Корреляционный анализ в EXCEL

Формула для вычислений	Функция EXCEL или инструмент Анализа данных
Оценка параметров модели парной регрессии	ЛИНЕЙН(изв_знач_у; зв_знач_х; константа; стат) Смысл аргументов функции изв_знач_у – диапазон значений у; изв_знач_х – диапазон значений х; константа – устанавливается на 0, если заранее известно, что свободный член равен 0 и на 1 в противном случае; стат– устанавливается на 0, если не нужен вывод дополнительных сведений регрессионного анализа и на 1 в противном случае.

Практическое занятие «Проверка адекватности модели».

Цель работы: Изучение t-критерия Стьюдента.

Чтобы определить насколько полученное уравнение регрессии значимо для всей совокупности, необходимо проверить:

• Определение значимости модели

• Установление наличия или отсутствия систематической ошибки.

Проверка значимости отдельных коэффициентов регрессии проводится по t-критерию Стьюдента путем проверки гипотезы о равенстве нулю каждого коэффициента регрессии.

Расчетные значения t -критерия сравнивают с табличным значением критерия, которое определяется при (n-k-1) степенях свободы и соответствующем уровне значимости α.

n – число уравнений,

k – число переменных,

α = 0,05 при доверительной вероятности 0,95 .

Формула для определения t-критерия Стьюдента:

,,

где Sa0 и Sa1 – стандартные отклонения свободного члена и коэффициента регрессии.

Определяются по формулам:

=
,
=
.

Задание: Рассчитать t-критерий Стьюдента по данным в табл.3 и сделать выводы о значимости отдельных коэффициентов уравнения регрессии.

0,636263125

a0=

-109

ε 2

( x_i – х_ср. ) 2

1

3357

2425

2027

2

3135

2050

1886

3

2842

1683

1700

4

3991

2375

2431

5

2293

1167

1350

6

3340

1925

2017

7

3089

1042

1857

8

4372

2925

2673

9

3563

2200

2158

10

3219

1892

1940

11

3308

2008

1996

12

3724

2225

2261

13

3416

1983

2065

14

3022

2342

1814

15

3383

2458

2044

16

4267

2125

2606

Сумма

Расчет t-критерий Стьюдента можно также произвести с помощью Excel, используя стандартную функцию, приведенную в таблице 4.

Оценка параметров модели парной и множественной линейной регрессии.

Сервис / Анализ данных Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессия

Оценка значимости коэффициента парной корреляции с использованием t – критерия Стьюдента. Вычисленное по этой формуле значение t_набл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-2).

СТЬЮДРАСПОБР (вероятность; степени_свободы) Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента. Степени_свободы — число степеней свободы, характеризующее распределение.

Сделать выводы о значимости коэффициентов уравнения регрессии.

Практическое занятие «Определение значимости модели по F – критерию Фишера»

Цель работы: Изучение F- критерия Фишера.

Для проверки значимости уравнения регрессии в целом используется F – критерий Фишера.

В случае парной линейной регрессии критерий определяется:

= (n-k-1) (6).

Если при заданном уровне значимости расчетное значение F – критерий Фишера с γ 1= k , γ 2 = n – k -1 степенями свободы больше табличного, то модель считается значимой

Задание: Используя данные предыдущей работы, рассчитать F- критерий Фишера и сделать выводы.

Для расчета следует воспользоваться инструментом Регрессия из пакета Сервис / Анализ данных и выбрать значение.

Расчет F-критерий Фишера можно также произвести с помощью Excel, используя стандартную функцию (см. табл.5)

Оценка параметров модели парной и множественной линейной регрессии.

Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессия
Проверка значимости модели регрессии с использованием F-критерий Фишера

FРАСПОБР(вероятность; степени_свободы1; степени_свободы2) Вероятность — это вероятность, связанная с F-распределением. Степени_свободы 1 — это числитель степеней свободы-n1= k. Степени_свободы 2 — это знаменатель степеней свободы-.n2 = (n – k – 1), где k – количество факторов, включенных в модель,

Дата добавления: 2019-07-15 ; просмотров: 110 ;

Как рассчитать коэффициент корреляции

Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.

Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.

Расчет с помощью электронных таблиц Microsoft Excel

Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.

Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».

Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.

Далее нажимаем галочку (то есть, рассчитать) и получаем значение , в нашем случае 0,038. Как видим, коэффициент не равен нулю, хотя и очень близок к нему.

В таблицах Excel реализована формула расчета только коэффициента Пирсона.

Расчет с помощью программы STATISTICA

Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.

Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.