Котангенс

Тригонометрические формулы сложения углов

cos (α — β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α — β) = sin α · cos β — sin β · cos α 
cos (α + β) = cos α · cos β — sin α · sin β 

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Определение тангенса угла

Определение:

Тангенсом угла  называется отношение синуса угла  к косинусу угла 

Например,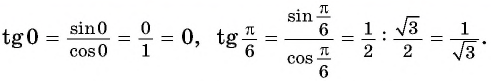 
Используя определение тангенса угла и значения синуса и косинуса этого угла, найдем также значения тангенсов углов 

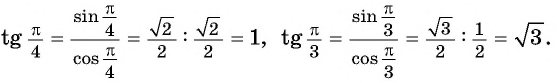
Поскольку  не существует.

Через точку  проведем прямую, перпендикулярную оси абсцисс, и продолжим луч  до пересечения с этой прямой в точке  (рис. 52). Получим треугольник  подобный треугольнику 

Из подобия треугольников  запишем равенство отношений их сторон: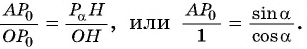 

Поскольку  то ордината точки  равна тангенсу угла 

Прямая, перпендикулярная оси абсцисс, проходящая через точку  называется осью тангенсов.

Нахождение тангенса произвольного угла

Для того чтобы найти тангенс произвольного угла а с помощью оси тангенсов, нужно:

1. Построить точку  на единичной окружности.
2. Продолжить прямую  до пересечения с осью тангенсов.
3. Найти ординату точки пересечения прямой  с осью тангенсов.

Найдите тангенс угла 

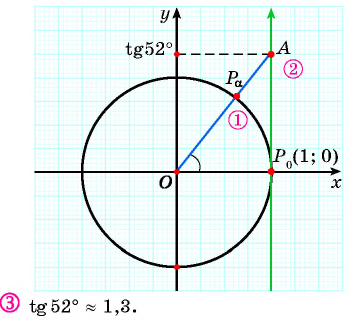
Значения тангенса произвольного угла с помощью оси тангенсов можно указать только приближенно. Для нахождения значения тангенса произвольного угла используют четырехзначные таблицы значений тангенса (синуса, косинуса)* или калькулятор. Методы высшей математики позволяют вычислять значения тангенса (синуса, косинуса) с любой заданной степенью точности.
 

Определите с помощью оси тангенсов:

Решение:

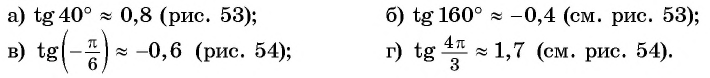
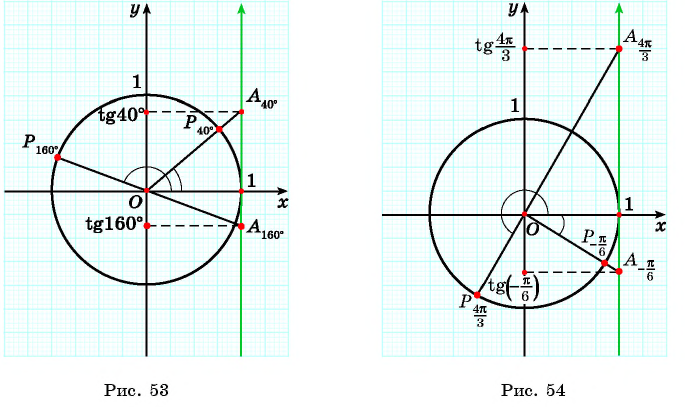
Пример №2

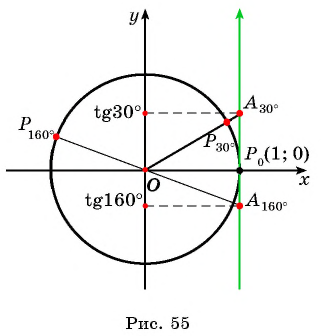
С помощью оси тангенсов сравните значения выражений 

Решение:

Отметим на оси тангенсов точки, соответствующие углам  (рис. 55), и сравним ординаты этих точек. Ордината точки  больше ординаты точки  значит, 

Для углов  тангенс не существует, так как косинусы этих углов равны нулю. Например,  не существуют.
Построим точку  единичной окружности поворотом точки  вокруг начала координат на угол  Рассмотрим прямоугольный треугольник , в котором гипотенуза  равна 1 (радиусу единичной окружности), а его катеты равны:  (рис. 56).

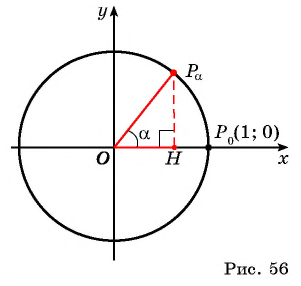
По определению котангенса острого угла получим: 

История

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.

Термины «тангенс» (от лат. «tangens» — касающийся) и «секанс» (лат. «secans» — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)

Как рассчитывается?

Процедура разработки этих производных довольно проста. Все, что вам нужно сделать, это правильно определить аргумент и тип функции, которую он представляет.

Например, выражение Ctg (f / g) имеет деление в своем аргументе. Это потребует дифференциации относительно U / V после определения производной котангенса.

Котангенс — это величина, обратная касательной. Алгебраически это означает, что:

(1 / tg x) = ctg x

Ctg x = Cos x / Sen x

Неверно говорить, что функция котангенса является «обратной» касательной. Это потому, что функция арктангенса по определению является арктангенсом.

(Тг-1 x) = arctg x

Согласно тригонометрии Пифагора, котангенс участвует в следующих разделах:

Ctg x = (cos x) / (sin x)

Ctg2 x + 1 = Csc2 Икс

Согласно аналитической тригонометрии, он отвечает следующим тождествам:

Ctg (a + b) = (1 — tg a. Tg b) / (tg a + tg b)

Ctg (a — b) = (1 + tg a. Tg b) / (tg a — tg b)

Ctg (2a) = (1 — tg2 а) / (2тг а)

Арктангенс и арккотангенс − теория, примеры и решения

Функция арктангенс и ее график

Функция тангенс определена в интервале кроме точек , … и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции тангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arctg y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арктангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арктангенс.

1. Область определения функции: .
2. Область значений функции: .
3. Функция является нечетной: .
4. Функция возрастает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале для уравнения (2) существует одно t, для которого tg t=a. Это решение

Следовательно в интервале уравнение (2) имеет один корень. Так как тангенс периодичная функция с основным периодом π, то все корни уравнения (2) отличаются на πn (n∈Z), т.е.

Решение уравнения (2) представлен на Рис.3:

Так как tg t − это ординат точки пересечения прямой OM_t1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OT_t пересекается с окружностью с радиусом 1 в двух точках: . Но только точка соответствует интервалу , которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Используя онлайн калькулятор получим:

Функция арккотангенс и ее график

Как известно, функция котангенс определена в интервале кроме точек -2π, —π 0, π, 2π,… и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arcctg y. Поменяв местами x и y, получим:

Функция (4) − это функция, обратная к функции

График функции арккотангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арккотангенс.

1. Область определения функции: .
2. Область значений функции: .
3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
4. Функция убывает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:

Решения уравнения (5) можно представить на единичной окружности (Рис.6):

ctg t − это абсцис точки пересечения прямой с прямым y=1. Любому числу a на линии котангенс соответствует только одна точка . Прямая пересекется с единичной окружностью в двух точках . Но только точка соответствует интервалу (0; π), которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (6):

Так как в интервале (0; π), то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (6), имеем

С помощью онлайн калькулятора вычисляем . Тогда

Доказательство по определению производной

Следующее выражение соответствует производной по определению. Если расстояние между двумя точками функции приближается к нулю.

Подставляя котангенс, получаем:

Идентичности применяются для суммы аргументов и взаимности

Дробь в числителе традиционно оперируется

Исключая противоположные элементы и беря общий множитель, получаем

Применяя пифагорейские тождества и взаимность, мы должны

Элементы, вычисленные в x, являются постоянными по отношению к пределу, поэтому они могут оставить аргумент this. Затем применяются свойства тригонометрических пределов.

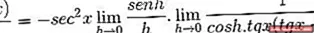
Лимит оценивается

Затем он факторизуется, пока не будет достигнуто желаемое значение.

Таким образом, производная котангенса противоположна квадрату косеканса.

презентация потеме Функция тангенса, ее график и свойства. презентация к уроку по алгебре (10 класс) по теме

Слайд 1

Функция у = tg х и построение ее графика. .

Слайд 3

Определяем цели учебной деятельности 1.Выделите слова и словосочетания, встречаемые впервые. 2.Определите, знаете ли Вы точное значение этих слов, а также тех слов и словосочетаний, которые уже встречались Вам, но точные их значения и определения остаются Вам пока неизвестными.

Слайд 4

Определяем цели учебной деятельности 3 . Какие новые определения и значения каких понятий необходимо будет усвоить в рамках изучения данной темы? 4. Какие умения нужно будет выработать? 5. Какие правила, алгоритмы, способы действий Вам неизвестны , и для решения каких задач они Вам будут нужны?

• Слайд 5
• Тангенс.
• Слайд 6

Предполагаемые цели учебной деятельности учеников 1. Определение функции тангенса, свойств этой функции 2.Построение графика функции тангенс по таблице значений и тем свойствам, которые известны для тангенса (алгоритм построения). Узнать, н а какой линии находятся тангенсы углов.

Слайд 7

Находим ответы на вопросы в учебнике. Стр.17 -стр.18: определение , л иния тангенсов углов, о бласть определения, о бласть значений, с войства тангенса, известные вам на сегодняшний день.

1. Слайд 8
2. Рисунок 10 из учебника
3. Слайд 9

Функция у = tg х. Определение. Числовая функция, заданная формулой у = tg х , называется функцией тангенса. Тангенс угла – отношение ординаты точки на единичной окружности, соответствующей данному углу, к абсциссе этой точки. А где находятся тангенсы углов?

• Слайд 10
• Тригонометрический круг
• Слайд 11
• диктант a = 185 градусов a = – 185 градусов a = 102 a = – 102 a = 250 a = – 250 a = 375 a = 145 a = – 145 a = 225 a = – 315 a = 210 a = 590 a = – 15 1Углом какой четверти является угол a , если:
• Слайд 12

диктант 2. Вычислите : 1 вариант. cos 180 + 5sin 90 sin 180 – 3 cos 0 5ctg 90 – 7tg 180 sin 60 + cos 30 2 вариант. cos 0 + 3sin 90 sin 270 – 2cos 180 6tg 180 + 2ctg 90 1 + ctg 270 – 5 tg 360

Слайд 13

Нормы оценок 1.Все задания верны – оценка «5» 2. 1-2 ошибки – оценка «4» 3. 3- 5 ошибок – оценка «3» 4. более 5 ошибок – беру дополнительное домашнее задание. Успехов в учебе!

Слайд 14

Ответы к диктанту. 1вариант. 1. III,II,II,III,III,II,I. 2. 4,-3,0. 2 вариант. 1.II,III,III,I,III,III,IV. 2. 0,2,4. Задание . Заполнить в тетради таблицу значений для построения графика у = tg х. Работа в парах.

Слайд 15

Построение графика. Составляем план построения графика, пользуясь учебником.

Слайд 16

План построения графика. 1 . Правильно выбери единичный отрезок. 2. Н айди область определения. 3 Проведи прямые у = π/ 2 + π n , где n принадлежит целым числам. 4. Построй график. Работаем в парах.

1. Слайд 17
2. Линия тангенса
3. Слайд 18
4. График функции в 1 четверти у = tg x x y 0 1
5. Слайд 19
6. у = tg x х у y = tg x
7. Слайд 20

Выполнение заданий. №37(В),33(г). Устно составить план выполнения задания, обговорить в парах. Рефлексия. Ответьте на вопросы: Какие новые знания вы приобрели на этом уроке? Какие новые умения? Все ли цели урока были достигнуты? .

Слайд 21

Домашняя работа. 1. Построить по аналогичному график функции котангенс. 2.Уметь доказывать по рис 10 из учебника, что касательная к числовой окр ., проведенная в точке (1,0), является линией тангенсов.

36( а,б,в ),38(а), 39( а,в,г ) Творческое задание. По рис.11учебника, доказать, что касательная прямая, проведенная в точке (0,1) к числовой окружности, является линией котангесов . Спасибо за урок.

Слайд 22

Спасибо за урок.

Тригонометрические функции в прямоугольном треугольнике

Чтобы определить тригонометрические функции произвольного угла возьмём произвольный прямоугольный треугольник, содержащий угол . Стороны этого треугольника мы будем называть так:

• Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона
• Противолежащий катет — катет, лежащий напротив угла. Например, катет — противолежащий по отношению к углу
• Прилежащий катет — катет, являющийся стороной угла. Например, катет — прилежащий по отношению к углу

Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна Это означает, что углы между катетами и гипотенузой лежат между и Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.

Си́нус угла — отношение противолежащего катета к гипотенузе: Это отношение не зависит от выбора треугольника , содержащего угол так как все такие треугольники подобны.

Ко́синус угла — отношение прилежащего катета к гипотенузе: Так как синус одного острого угла в треугольнике равна косинусу второго, и наоборот.

Та́нгенс угла — отношение противолежащего катета к прилежащему:

Кота́нгенс угла — отношение прилежащего катета к противолежащему: Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.

Се́канс угла — отношение гипотенузы к прилежащему катету:

Косе́канс угла — отношение гипотенузы к противолежащему катету:

Из определений тригонометрических функций следует:

и симметрично:

Ссылки

1. Тригонометрические ряды, Том 1. А. Зигмунд. Издательство Кембриджского университета, 2002 г.
2. Исчисление одной переменной. Рон Ларсон, Брюс Х. Эдвардс. Cengage Learning, 10 ноября 2008 г.
3. Исчисление с тригонометрией и аналитической геометрией. Джон Х. Саксон, Джон Саксон, Фрэнк Ван, Дайана Харви. Саксонские издательства, 1988 г.
4. Многопараметрический анализ. Сатиш Ширали, Харкришан Лал Васудева. Springer Science & Business Media, 13 декабря. 2010 г.
5. Системная динамика: моделирование, моделирование и управление мехатронными системами. Дин К. Карнопп, Дональд Л. Марголис, Рональд К. Розенберг. John Wiley & Sons, 7 марта 2012 г.
6. Исчисление: математика и моделирование. Уильям Баулдри, Джозеф Р. Фидлер, Фрэнк Р. Джордано, Эд Лоди, Рик Витрей. Эддисон Уэсли Лонгман, 1 января 1999 г.

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.

Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.

Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.

Поведение

Это нечетная функция, поскольку Ctg (-x) = — Ctg x. Таким образом, известно, что функция представляет собой симметрию относительно начала координат. Он также представляет уменьшение каждого интервала, расположенного между двумя последовательными вертикальными асимптотами.

Он не имеет максимальных или минимальных значений, потому что его приближения к вертикальным асимптотам представляют поведение, при котором функция увеличивается или уменьшается бесконечно.

Нули или корни функции котангенса находятся в нечетных кратных π / 2. Это означает, что Ctg x = 0 выполняется для значений вида x = nπ / 2 с n нечетным целым числом.