Методы числовых объектов

Поля

AwayFromZero	1	Стратегия округления до ближайшего числа, а если число находится на расстоянии от двух других, оно округляется в сторону ближайшего числа, которое находится вне нуля.
ToEven	Стратегия округления до ближайшего числа, а если число находится на расстоянии от двух других, оно округляется в сторону ближайшего четного числа.
ToNegativeInfinity	3	Стратегия нисходящей, направленная вниз, с результатом, наиболее близким к и не превышающим бесконечно точный результат.
ToPositiveInfinity	4	Стратегия сквозного округления с результатами, ближайшей к и не меньше бесконечно точных результатов.
ToZero	2	Стратегия направленного округления в сторону нуля с результатом, наиболее близким к и не превышающим точность, чем бесконечное значение.

Сравнение чисел

Для сравнения чисел в JavaScript используются следующие операторы: == (равно), != (не равно), > (больше), = (больше или равно),

Например, сравним два числа:

Console.log(2>3); //false
console.log(5>=3); //true

При сравнении чисел с дробной частью необходимо учитывать погрешности, которые могут возникать во время этих вычислений.

Например, в JavaScript сумма чисел (0.2 + 0.4) не равна 0.6:

Console.log((0.2+0.4)==0.6); //false

Погрешности происходят потому что все вычисления компьютер или другое электронное устройство производит в 2 системе счисления. Т.е. перед тем как выполнить какие-то действия компьютер сначала должен преобразовать представленные в выражении числа в 2 систему счисления. Но, не любое дробное десятичное число можно представить в 2 системе счисления точно.

Например, число 0.25 10 в двоичную систему преобразуется точно.

0.125 × 2 = 0.25 | 0
0.25 × 2 = 0.5 | 0
0.5 × 2 = 1 | 1
0.125 10 = 0.001 2

Например, число 0.2 10 можно преобразовать в 2 систему только с определённой точностью:

0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
…
0.2 10 = 0.001100110011… 2

В результате эти погрешности скажутся при вычисления суммы двух чисел и результатах сравнения. Т.е. получится что на самом деле JavaScript будет видет эту запись следующим образом:

0.6000000000000001==0.6

При вычислениях или отображении чисел с дробной частью необходимо всегда указывать точность, с которой это необходимо делать.

Например, сравнить числа до 2 знаков после запятой используя методы toFixed() и toPrecision() :

//метод toFixed()
console.log((0.2+0.4).toFixed(2)==(0.6).toFixed(2)); //true
//метод toPrecision()
console.log((0.2+0.4).toPrecision(2)==(0.6).toPrecision(2)); //true

Основные математические операции

В JavaScript существуют следующие математические операторы: + (сложение), — (вычитание), * (умножение), / (деление), % (остаток от деления), ++ (увелить значение на 1), — (уменьшить значение на 1).

6+3 //9
6-3 //3
6*3 //18
6/3 //2
6%3 //0, т.е. 6:3=2 => 6-3*2 => ост(0)
5%2 //1, т.е. 5:2=2(.5) => 5-2*2 => ост(1)
7.3%2 //1.3, т.е. 7.3:2=3(.65) => 7.3-2*3 => ост(1.3)
//знак результата операции % равен знаку первого значения
-9%2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-9%-2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-2%5 //-2, т.е. 2:5=0(.4) => 2-5*0 => ост(2)
x = 3;
console.log(x++); //выводит 3, у уже потом устанавливает 4
console.log(x); //4
x = 3;
console.log(++x); //устанавливает 4 и выводит
x = 5;
console.log(x—); //выводит 5, у уже потом устанавливает 4
console.log(x); //4
x = 5;
console.log(—x); //устанавливает 4 и выводит
Кроме этого в JavaScript есть комбинированные операторы: x+=y (x=x+y), x-=y (x=x-y), x*=y (x=x*y), x/=y (x=x/y), x%=y (x=x%y).
x = 3;
y = 6;
x+=y;
console.log(x); //9
x = 3;
y = 6;
x-=y;
console.log(x); //-3
x = 3;
y = 6;
x*=y;
console.log(x); //18
x = 3;
y = 6;
x/=y;
console.log(x); //0.5
x = 3;
y = 6;
x%=y;
console.log(x); //3

Целая и дробная часть числа

Получить целую часть числа можно используя метод Math.floor() и parseInt() :

Console.log(Math.floor(7.21)); // 7
console.log(parseInt(7.21)); // 7

Получить дробную часть числа можно воспользовавшимся оператором процент (%). Данный оператор возвращает остаток, который будет получен от деления первого числа на второе. В данном случае в качестве 2 числа необходимо использовать 1.

Console.log(7.21%1); // 0.20999999999999996
// с точностью до 2 знаков после запятой
console.log((7.21%1).toFixed(2)); // «0.21»

Кроме этого дробную часть можно получить также с помощью вычислений:

Var number = 7.21;
var fractionNumber = number — Math.floor(Math.abs(number));
console.log(fractionNumber); // 0.20999999999999996

Делится ли число нацело

Определить делится ли число нацело можно используя оператор процента:

Var number = 9;
// если остаток от деления числа number на 3 равен 0, то да, иначе нет
if (number%3==0) {
console.log («Число » + number + » делится на 3″);
} else {
console.log («Число » + number + » не делится на 3″);
}

Работа с округленными числами

Округление уже округленных чисел

Если исходное число уже является результатом округления, то для пограничного случая, когда новая цифра округления равна 5 (и все цифры после этого нуля), по возможности следует использовать неокругленное число (например, с математическими константами):

Известное неокругленное число: 13.374999747, округленное начальное число: 13.3750

→ число округлено: 13,37

Неокругленное число неизвестно, начальное число округлено: 13.3750

→ округленное число: 13,38.

Идентификация результатов округления

В научных статьях и таблицах логарифмов иногда указывается, была ли последняя цифра получена округлением в большую или меньшую сторону. Число, полученное округлением в большую сторону, обозначается линией под (или над) числом, число, которое не было изменено округлением (число было округлено), отмечается точкой над числом.

Примеры:

• 3,4134928 …{\ displaystyle 3 {,} 4134928 …}становится к ; это число — новые раунды . При повторном округлении (в примере до трех знаков после запятой) необходимо округлять в меньшую сторону.3,4135_{\ displaystyle 3 {,} 413 {\ underline {5}}}3,413{\ displaystyle 3 {,} 413}
• 2,6245241 …{\ displaystyle 2 {,} 6245241 …}становится к ; это число станет яснее при следующем округлении до . При повторном округлении (в примере до трех знаков после десятичной точки) вам необходимо округлить в большую сторону. Для дальнейшего округления (здесь до двух мест) оно будет округлено в меньшую сторону, обозначенное цифрой 5 .2,6245˙{\ displaystyle 2 {,} 624 {\ dot {5}}}2,625{\ displaystyle 2 {,} 625}2,625_{\ displaystyle 2 {,} 62 {\ underline {5}}}

Если другие цифры не известны, предполагается, что начальный номер является точным.

Расчет с округленными числами

Если в расчет включены округленные числа, окончательный результат должен быть округлен до того же количества значащих цифр. Если z. Например, если измеряется сила 12,2 Ньютона, все окончательные результаты, зависящие от этой силы, должны быть округлены так, чтобы осталось не более трех значащих цифр. Таким образом, читатель не претендует на то, чтобы быть более точным, чем то, что на самом деле доступно.

Применения

Округление используется для того, чтобы работать с числами в пределах того количества знаков, которое соответствует реальной точности параметров вычислений (если эти значения представляют собой измеренные тем или иным образом реальные величины), реально достижимой точности вычислений либо желаемой точности результата. В прошлом округление промежуточных значений и результата имело прикладное значение (так как при расчётах на бумаге или с помощью примитивных устройств типа абака учёт лишних десятичных знаков может серьёзно увеличить объём работы). Сейчас оно остаётся элементом научной и инженерной культуры. В бухгалтерских приложениях, кроме того, использование округлений, в том числе промежуточных, может требоваться для защиты от вычислительных ошибок, связанных с конечной разрядностью вычислительных устройств.

Более того, некоторые исследования используют округления возраста для измерения числовой грамотности. Это связано с фактом, что менее образованные люди склонны округлять свой возраст вместо того, чтобы указывать точный. Например, в официальных записях населения с более низким уровнем человеческого капитала чаще встречается возраст 30, чем 31 или 29.

JavaScript

JS Array
concat()
constructor
copyWithin()
entries()
every()
fill()
filter()
find()
findIndex()
forEach()
from()
includes()
indexOf()
isArray()
join()
keys()
length
lastIndexOf()
map()
pop()
prototype
push()
reduce()
reduceRight()
reverse()
shift()
slice()
some()
sort()
splice()
toString()
unshift()
valueOf()

JS Boolean
constructor
prototype
toString()
valueOf()

JS Classes
constructor()
extends
static
super

JS Date
constructor
getDate()
getDay()
getFullYear()
getHours()
getMilliseconds()
getMinutes()
getMonth()
getSeconds()
getTime()
getTimezoneOffset()
getUTCDate()
getUTCDay()
getUTCFullYear()
getUTCHours()
getUTCMilliseconds()
getUTCMinutes()
getUTCMonth()
getUTCSeconds()
now()
parse()
prototype
setDate()
setFullYear()
setHours()
setMilliseconds()
setMinutes()
setMonth()
setSeconds()
setTime()
setUTCDate()
setUTCFullYear()
setUTCHours()
setUTCMilliseconds()
setUTCMinutes()
setUTCMonth()
setUTCSeconds()
toDateString()
toISOString()
toJSON()
toLocaleDateString()
toLocaleTimeString()
toLocaleString()
toString()
toTimeString()
toUTCString()
UTC()
valueOf()

JS Error
name
message

JS Global
decodeURI()
decodeURIComponent()
encodeURI()
encodeURIComponent()
escape()
eval()
Infinity
isFinite()
isNaN()
NaN
Number()
parseFloat()
parseInt()
String()
undefined
unescape()

JS JSON
parse()
stringify()

JS Math
abs()
acos()
acosh()
asin()
asinh()
atan()
atan2()
atanh()
cbrt()
ceil()
clz32()
cos()
cosh()
E
exp()
expm1()
floor()
fround()
LN2
LN10
log()
log10()
log1p()
log2()
LOG2E
LOG10E
max()
min()
PI
pow()
random()
round()
sign()
sin()
sinh()
sqrt()
SQRT1_2
SQRT2
tan()
tanh()
trunc()

JS Number
constructor
isFinite()
isInteger()
isNaN()
isSafeInteger()
MAX_VALUE
MIN_VALUE
NEGATIVE_INFINITY
NaN
POSITIVE_INFINITY
prototype
toExponential()
toFixed()
toLocaleString()
toPrecision()
toString()
valueOf()

JS OperatorsJS RegExp
Modifiers:
g
i
m
Groups:

(x|y)
Metacharacters:
.
\w
\W
\d
\D
\s
\S
\b
\B
\0
\n
\f
\r
\t
\v
\xxx
\xdd
\uxxxx
Quantifiers:
+
*
?
{X}
{X,Y}
{X,}
$
^
?=
?!
Properties:
constructor
global
ignoreCase
lastIndex
multiline
source
Methods:
compile()
exec()
test()
toString()

JS Statements
break
class
continue
debugger
do…while
for
for…in
for…of
function
if…else
return
switch
throw
try…catch
var
while

JS String
charAt()
charCodeAt()
concat()
constructor
endsWith()
fromCharCode()
includes()
indexOf()
lastIndexOf()
length
localeCompare()
match()
prototype
repeat()
replace()
search()
slice()
split()
startsWith()
substr()
substring()
toLocaleLowerCase()
toLocaleUpperCase()
toLowerCase()
toString()
toUpperCase()
trim()
valueOf()

Round(Decimal)

Math.Round(d) rounds a decimal value to the nearest integral value, and rounds midpoint values to the nearest even number.

Syntax

The syntax of Round(d) method is

Math.Round(Decimal d)

where

Parameter	Description
d	The decimal number to be rounded.

Return Value

The method returns rounded Decimal value.

Example 1 – Round(d)

In this example, we will take some decimal values and round them to the nearest integral values using Math.Round() method.

C# Program

using System;
 
class Example {
    static void Main(string[] args) {
        Decimal d, result;

        d = 10.2563M;
        result = Math.Round(d);
        Console.WriteLine($"Round({d}) = {result}");

        d = 10.63M;
        result = Math.Round(d);
        Console.WriteLine($"Round({d}) = {result}");

        d = 10.5M;
        result = Math.Round(d);
        Console.WriteLine($"Round({d}) = {result}");
    }
}

Output

Round(10.2563) = 10
Round(10.63) = 11
Round(10.5) = 10

Округление с помощью эпсилона

Альтернативный метод JavaScript, позволяющий осуществить округление до десятых, был введен в ES6 (также известном, как JavaScript 2015). «Машинный эпсилон» обеспечивает разумный предел погрешности при сравнении двух чисел с плавающей запятой. Без округления, сравнения могут дать результаты, подобные следующим:

0.1 + 0.2 === 0.3
> false

Math.EPSILON может быть использован в функции для получения корректного сравнения:

function epsEqu(x, y) {
    return Math.abs(x - y) < Number.EPSILON * Math.max(Math.abs(x), Math.abs(y));
}

Функция принимает два аргумента: один содержит вычисления, второй ожидаемый (округленный) результат. Она возвращает сравнение этих двух параметров:

epsEqu(0.1 + 0.2, 0.3)
> true

Все современные браузеры поддерживают математические функции ES6. Но если необходимо обеспечить поддержку в старых браузерах, то нужно использовать полифиллы.

Важные заметки о числах

Для начала запомните, что в js все виды чисел (дробные и целые) относятся к типу Number
. К тому же все они 64-битные, так как хранятся в формате «double precision», который также известен под стандартом IEEE-754.

Создаются численные переменные привычным способом:

Поддерживает и другие числовые представления. Так, еще можно создавать числа с плавающей точкой (их еще иногда называют «числа в научном формате»).

В появилась поддержка очень интересного метода toLocaleString ()
, который форматирует все числовые параметры по спецификациям, прописанным в ECMA 402. Благодаря этому большие числа, телефонные номера, валюты и даже проценты красиво выводятся в диалоговом окне.

Для работы с элементами типа Number был предусмотрен целый глобальный объект с кучей всевозможных математических функций, имя которого Math
.

Помимо этого, существуют и другие методы, которые выполняют округление числовых значений до целых чисел, до десятых, сотых и т.д. Рассмотрим их все подробнее.

Оператор Round

А вы знаете, что при использовании для округления чисел в VBA Excel оператора Round, вы можете получить совершенно не тот результат, который ожидали? И ведь это действительно так!

Скопируйте в модуль VBA следующую процедуру и запустите ее выполнение:

1 2 3 4 5 6 7 8 9 10 11

SubTest_1() Dima1 AsSingle,a2 AsSingle,a3 AsSingle,a4 AsSingle a1=Round(1.5,) a2=Round(2.5,) a3=Round(3.5,) a4=Round(4.5,) MsgBox»Round(1.5, 0)=»&a1&vbNewLine&_ «Round(2.5, 0)=»&a2&vbNewLine&_ «Round(3.5, 0)=»&a3&vbNewLine&_ «Round(4.5, 0)=»&a4 EndSub

В результате вы получите это:

Удивительно, не правда ли? Как же так получилось?
Дело в том, что оператор Round осуществляет «бухгалтерское» (или «банковское») округление, которое призвано при большом количестве таких операций свести погрешность к минимуму. Это достигается за счет того, что оператор Round использует при округлении правило, отличное от того, которое мы знаем еще со школы, когда округляемое число увеличивается на единицу, если отбрасываемое число равно пяти. Суть округления с помощью оператора Round состоит в том, что если перед отбрасываемой пятеркой стоит нечетная цифра, то она увеличивается на единицу (округление вверх), а если перед ней стоит четная цифра, то она не увеличивается (округление вниз).

Еще можно сформулировать «бухгалтерское» округление так: при отбрасывании пятерки число округляется к ближайшему четному

Обратите внимание, что в результатах нашего примера все полученные числа — четные.
Проверим погрешность:

1. Сумма исходных чисел: 1.5 + 2.5 + 3.5 +4.5 = 12
2. Сумма округленных чисел: 2 + 2 + 4 + 4 = 12

Результат получился просто идеальный для приведенного примера, так как суммы исходных и округленных чисел равны.

Для чего округлять числа?

JavaScript не хранит целые числа, поскольку их значения представлены в виде цифр с плавающей точкой. Многие дроби не могут быть представлены числом с определенным конечным количеством знаков после запятой, поэтому JavaScript может генерировать результаты, наподобие приведенного ниже:

0.1 * 0.2;
> 0.020000000000000004

На практике это не будет иметь никакого значения, поскольку речь идет о погрешности в 2 квинтилионные. Но это может отразиться на результате при работе с числами, которые представляют значения валют, процентов или размер файла. Поэтому нужно сделать JavaScript округление до целых или до определенного знака после запятой.

Rounding the Number

Whatever your reason for rounding numbers may be, JavaScript has
several ways of allowing you to round numbers. Let us look at the most
common ones.

Rounding to the Nearest Integer

The most common function for rounding your value is the prom king
himself, Math.round:

Math.round(1.532); // 2
Math.round(1.235); // 1
Math.round(27.94); // 28
Math.round(0.0005); // 0

This function works by rounding your number to the nearest integer.
If the first number after the decimal is 5 or higher, it rounds up. If
the first number after the decimal is 4 or lower, it rounds down. The
Math.round function most closely
resembles what you may have learned in school.

Its equally popular variants are the
Math.floor and
Math.ceil functions. Whereas Math.round
would either round up or down depending on what the number after the
decimal is, Math.floor will always round
down to the next lowest integer regardless of what the value after the
decimal is. Similarly…in an opposite way,
Math.ceil will always round up to the next highest integer
regardless of what the value after the decimal actually is:

Math.ceil(1.5); // 2
Math.floor(1.5); // 1
Math.floor(1.235); // 1
Math.ceil(0.0005); // 1

All of this should look pretty straightforward. Just to drive the point
home about the next highest and lowest integers, let’s look what happens
when we are dealing with negative values:

Math.ceil(-45) // -45
Math.floor(-45) // -45
Math.ceil(-.5) // 0
Math.floor(-.5) // -1
Math.round(-45) // -45
Math.round(-.5) // -1
Math.round(-1.24) // -1
		

The Math.ceil and
Math.floor functions work as expected.
They round up or down to the next largest or smallest integer. Remember,
in the negative world, the smaller the absolute value of your number,
the larger its actual value:

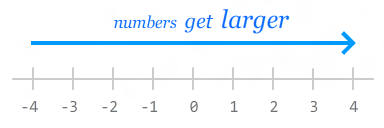
That is why rounding up from -.5
results in you getting . If you think
of the relative size of numbers as being on the number line,
Math.ceil goes right.
Math.floor goes left. It’s like opposite day over there.

Our prom king Math.round, though,
exhibits some slightly shallow behavior. Instead of rounding up or down
to the nearest large or small number, this function literally rounds up or
rounds down based on the absolute value of the number. That is why
rounding -.5 is actually a
-1 (a smaller number) than being 0 like
you may expect.

Rounding to Arbitrary Levels of Precision

In the previous section, you learned how you can round to the nearest
integer. There will be times when you want to round to a particular
decimal position for extra preciseness. Let’s say we want to round our value of Pi to just 2 digits past the
decimal point. In other words, we want 3.14159
to be rounded off to 3.14. Using the
three amigos (Math.round,
Math.floor, and
Math.ceil) without any modification will cause our value to either
be 3 or 4. That’s not what we want.

To get what we want, there is a simple approach we can take made up of just three steps:

1. To get X digits of precision, multiply our number by 10 to the power of X.
2. Round the result using Math.round()
3. Divide the new result by 10 to the power of X again.

To make this more concrete, let’s see we want to round 3.14159 to two digits of precision. To get two decimal positions of precision,
we can multiply our number by 10 to the power of two
(aka 100) and round that value:

Math.round(3.14159 * 100);

Next, divide the result of this rounding
operation by 10 to the power of two again to get
the answer you are looking for:

Math.round(3.14159 * 100) / 100; // result is 3.14

To generalize this a bit, here is a basic formula:

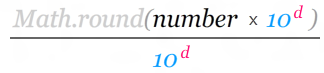
The d stands for the number of places after
the decimal point you want to go to. The number
is the value you are trying to round. Everything else should be
self-explanatory.

Using this model, here is how we can round 3.14159 to the tenths,
hundredths, thousandths, and ten thousandths positions:

Math.round(3.14159 * 10) / 10; // 3.1
Math.round(3.14159 * 100) / 100; // 3.14
Math.round(3.14159 * 1000) / 1000; // 3.142
Math.round(3.14159 * 10000) / 10000; // 3.1416

You can substitute Math.round with
Math.floor or
Math.ceil depending on what exactly you are going for, and the
behavior will be predictable.

Round(Double, Int32)

Math.Round(d, decimals) rounds a double-precision floating-point value to a specified number of fractional digits , and rounds midpoint values to the nearest even number.

Syntax

The syntax of Round(d, decimals) method is

Math.Round(Double d, Int32 decimals)

where

Parameter	Description
d	The double-precision floating-point number to be rounded.
decimals	The number of decimal places in the return value.

Return Value

The method returns rounded Double value.

Example 6 – Round(Double, Int32)

In this example, we will take some decimal double-precision floating-point numbers and round them to specific number of decimal points using Math.Round() method.

C# Program

using System;
 
class Example {
    static void Main(string[] args) {
        Double d, result;
        Int32 decimals;

        d = 10.2563;
        decimals = 2;
        result = Math.Round(d, decimals);
        Console.WriteLine($"Round({d}, {decimals}) = {result}");

        d = 10.63524;
        decimals = 1;
        result = Math.Round(d, decimals);
        Console.WriteLine($"Round({d}, {decimals}) = {result}");

        d = 10.5;
        decimals = 0;
        result = Math.Round(d, decimals);
        Console.WriteLine($"Round({d}, {decimals}) = {result}");
    }
}

Output

Round(10.2563, 2) = 10.26
Round(10.63524, 1) = 10.6
Round(10.5, 0) = 10

Целая и дробная часть числа

Получить целую часть числа можно используя метод Math.floor() и parseInt() :

Console.log(Math.floor(7.21)); // 7
console.log(parseInt(7.21)); // 7

Получить дробную часть числа можно воспользовавшимся оператором процент (%). Данный оператор возвращает остаток, который будет получен от деления первого числа на второе. В данном случае в качестве 2 числа необходимо использовать 1.

Console.log(7.21%1); // 0.20999999999999996
// с точностью до 2 знаков после запятой
console.log((7.21%1).toFixed(2)); // «0.21»

Кроме этого дробную часть можно получить также с помощью вычислений:

Var number = 7.21;
var fractionNumber = number — Math.floor(Math.abs(number));
console.log(fractionNumber); // 0.20999999999999996

Делится ли число нацело

Определить делится ли число нацело можно используя оператор процента:

Var number = 9;
// если остаток от деления числа number на 3 равен 0, то да, иначе нет
if (number%3==0) {
console.log («Число » + number + » делится на 3″);
} else {
console.log («Число » + number + » не делится на 3″);
}

Сравнение дробных чисел

У математических вычислений есть одна особенность — их результат не всегда абсолютно точный. Это проблема
не только JavaScript, но и большинства языков программирования. Так происходит потому, что числа и другие
данные переводятся в двоичный код, и только потом с ними производятся вычисления. В большинстве случаев это
не приводит к особенным трудностям, просто в результате расчётов иногда получается число с большим количеством
знаков после запятой. Но есть ситуация, когда неточность вычислений влияет на работу программы. Это сравнение
чисел. Если сравниваются разные числа, то здесь всё должно быть нормально.

5.1

Но если при вычислении получаются два одинаковых дробных числа, то результат их сравнения не предсказуем.
Они могут быть равны, либо одно может быть больше другого. Когда в скрипте
используется такое сравнение,
то нужно проверять, правильно ли работает скрипт. Если в нём есть ошибка, то нужно округлять значения, которые
сравниваются.

Функция isNaN

Функция isNaN
предназначена для определения того, является ли аргумент числом или может ли быть преобразован к нему. Если это так, то функция isNaN возвращает false. В противном случае она возвращает true.

IsNaN(NaN); //true
isNaN(«25px»); //true, т.к. 20px — это не число
isNaN(25.5); //false
isNaN(«25.5″); //false
isNaN(» «); //false, т.к. пробел или неcколько пробелов преобразуется к 0
isNaN(null); //false, т.к. значение null преобразуется к 0
isNaN(true); //false, т.к. значение true преобразуется к 1
isNaN(false); //false, т.к. значение false преобразуется к 0

Если это действие нужно выполнить без приведения типа, то используйте метод Number.isNaN
. Данный метод был введён в язык, начиная с ECMAScript 6.

Решение без знаков после запятой: javascript количество знаков после запятой

Если же знаки после запятой нужно полностью откинуть, то есть нужно округлить дробное число до целого, то можно использовать функции класса Math: round, ceil и floor.
Round — округляет в большую или меньшую сторону (в зависимости от числа). Если значение после запятой больше половины, то округлит в большую сторону, если меньше — в меньшую. То есть если 0.51 — станет 1, если 0.49 — 0.

Ceil — от англ. потолок округляет всегда в большую сторону.

Floor — от англ. пол округляет всегда в меньшую сторону.

Var num = 1538.9891200153;
num_str=Math.round(num); //num_str=1539;
num_str=Math.floor(num); //num_str=1538;
num_str=Math.ceil(num); //num_str=1539;

Часто вычисления дают результаты, которые не соответствуют пределам нужных диапазонов. В результате нужно осуществлять JavaScript округление
до определенного значения.

Великий и могучий Math

Глобальный объект Math включает в себя огромное количество разнообразных математических и тригонометрических функций. Это очень нужный объект и часто выручает разработчиков при работе с цифровыми данными.

На других платформах существуют аналогии Math. Например, в таких популярных языках, как Java и C#, Math представляет собой класс, который поддерживает все те же стандартные функции. Так что как видите этот инструмент действительно великий и могучий.

Теперь я хочу пройтись по конкретным методам, отвечающим за округление, и подробно о них рассказать.

Math.floor ()

Начну с Math.
floor

Обратите внимание на наименование метода. Логически становится понятно, что раз речь идет об округлении, а дословный перевод слова «floor» означает «пол», то данный инструмент округлит обрабатываемые значения в меньшую строну

Также возможен вариант, когда обработанное число с помощью этой функции осталось прежним. Все потому, что округление осуществляется по нестрогому неравенству (

в ответе будет число 4.

Math.ceil ()

Опять-таки посмотрите на название (в такой способ материал быстрее усваивается). Если кто-то не знает, то «ceil» означает «потолок». Значит округление числовых данных будет осуществляться в большую сторону, используя нестрогое неравенство (>=).

Как вы уже догадались, в ответе будет число 5.

Math.round ()

Данный метод округляет дробное число до ближайшего целого. Так, если дробная часть находится в диапазоне от 0 и до 0.5 не включительно, то округление происходит к меньшему значению. А если дробная часть находится в диапазоне от включительно 0.5 и до следующего целого числа, то она округляется к большему целому.

Надеюсь, все подумали или сказали правильный ответ – 5.

Round(Double)

Math.Round(d) rounds a double-precision floating-point value to the nearest integral value, and rounds midpoint values to the nearest even number.

Syntax

The syntax of Round(d) method is

Math.Round(Double d)

where

Parameter	Description
d	The double-precision floating-point number to be rounded.

Return Value

The method returns rounded Double value.

Example 5 – Round(d)

In this example, we will take some double-precision floating-point numbers and round them to the nearest integral values using Math.Round() method.

C# Program

using System;
 
class Example {
    static void Main(string[] args) {
        Double d, result;

        d = 10.2563;
        result = Math.Round(d);
        Console.WriteLine($"Round({d}) = {result}");

        d = 10.63;
        result = Math.Round(d);
        Console.WriteLine($"Round({d}) = {result}");

        d = 10.5;
        result = Math.Round(d);
        Console.WriteLine($"Round({d}) = {result}");
    }
}

Output

Round(10.2563) = 10
Round(10.63) = 11
Round(10.5) = 10

Why Round Numbers?

You may be wondering why anybody would want to go from having values
that are more precise to having values that are less precise. In this
section, we are going to look at some examples.

Displaying on the Pixel

Whenever you are doing anything on the canvas or positioning DOM elements using code, you’ll be doing a whole lot of pixel pushing to the screen. The things you are drawing on screen look best when its position and size values fall on a whole pixel. If you are using
fractional values, what you are displaying may end up looking blurry:

An easy way to ensure everything falls on pixel boundaries is to
round any position or size value to a whole number.

Improving Performance

Working with round numbers is faster
than having to deal with numbers that contain extra precision. Nuff said about that 😛

Dealing with JavaScript’s Quirky Number Handling

JavaScript stores all numbers internally as floating point values.
This means your calculations could be subject to floating point
shenanigans. Here is an example:

var blah = 0.2 * 0.4;

What do you think the value of blah actually is? If you guessed .08,
you would be wrong. Here is what actually shows up:

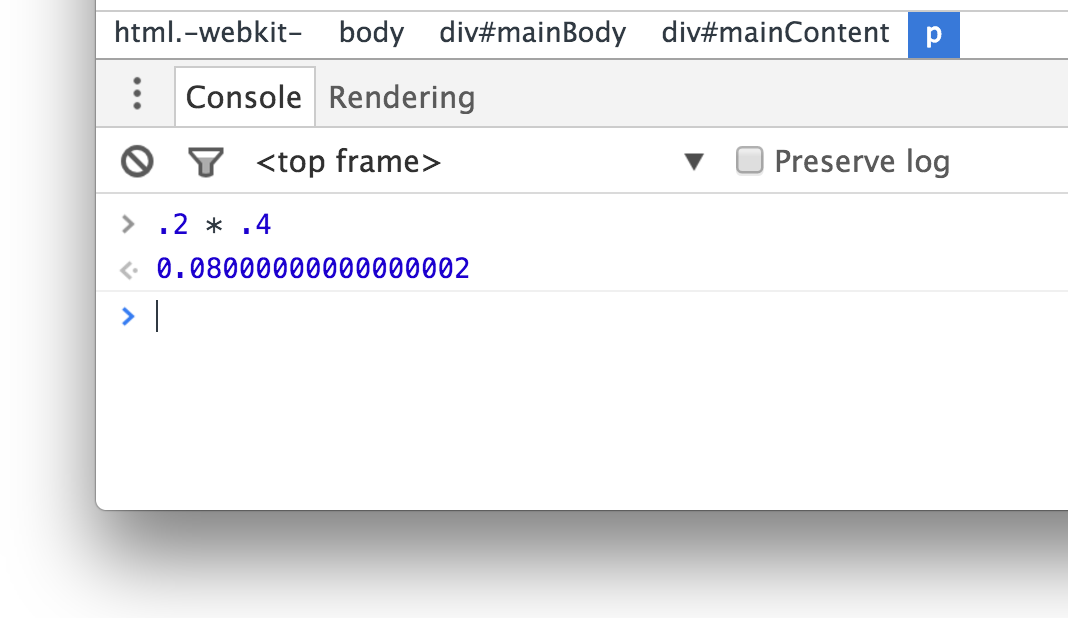
There is a reason why the 2 awkwardly shows up at the end of the result. It has to do with how
fractions are represented as floating point values. It is weird, but
that’s just how it is. By rounding your number, you can account for the unnecessary
precision and just get .08 like you probably wanted all along.