Коэффициент вариации excel

Расчет НМЦК в Excel начальной максимальной цены контракта

Для унификации подхода к формированию НМЦК (начальной (максимальной) цены контракта, подписываемого с единственным поставщиком) при выполнении закупок в соответствии с ФЗ №44 «О контрактной системе в сфере закупок товаров, работ, услуг для обеспечения государственных и муниципальных нужд» разработаны методические рекомендации с методами и формулами расчета. А для участия в государственных торгах нужно составлять обоснование НМЦК. Расчет можно произвести в Excel.

Исчисление и обоснование начальной (максимальной) цены контракта зависит от методов, определенных в Законе:

• метод сопоставимых рыночных цен (анализ рынка);
• нормативный;
• тарифный;
• проектно-сметный;
• затратный.

Предпочтение отдается методу сопоставимых рыночных цен. Получить ценовую информацию об одинаковых (идентичных) товарах, работах и услугах можно из следующих источников:

• официальных публикаций государственных и муниципальных органов, международных организаций;
• сайта госзакупок;
• сведений информационно-ценовых агентств;
• статистических отчетов;
• общедоступной рекламы в СМИ, Интернете.

При расчете начальной цены контракта используются коэффициенты, которые учитывают:

• объем товара, работ, услуг;
• срок определения НМЦК, исполнения договора;
• место поставки;
• изменение номенклатуры и т.д.

Расчетные данные и обоснование НМЦК оформляются документально и подписываются работником контрактной службы.



Выбор конкретного способа зависит от ситуации, исходных данных и других факторов.

Метод сопоставимых рыночных цен

НМЦК рассчитывается на основе информации о рыночных ценах на идентичные или однородные работы, товары или услуги. Собрать необходимые сведения законодатель предлагает следующими способами:

• отправить запросы не менее чем пяти поставщикам изучаемого товара;
• опубликовать запрос в ЕИС;
• найти данные в реестрах контрактов заказчиков;
• получить информацию из общедоступных источников.

Источники информации должны вызывать доверие и подтверждаться соответствующими расчетами.

Используемая формула:

, где

• v – объем товара;
• n – число значений в расчете;
• i – номер источника ценовой информации;
• цi– цена товара с номером i.

Рассмотрим пример расчета НМЦК в Excel.

На первом этапе собранные сведения заносятся в таблицу:

Запросы отправлены 5 поставщикам. Получен ответ от трех. Для получения объективной картины нужно не менее 3 цен от разных поставщиков. Это условие выполнено.

Далее нужно проверить однородность совокупности значений выявленных цен, которые применяются при расчете. Рассчитаем коэффициент вариации.

Как рассчитывается среднее квадратичное отклонение, показано на рисунке. Среднюю арифметическую цену считаем с помощью функции СРЗНАЧ (=СРЗНАЧ(E3:G3)). Для расчета коэффициента вариации среднее квадратичное отклонение делим на среднюю арифметическую цену: =I3/H3*100. Показатель не должен превышать 33%. Это условие соблюдено.

Теперь рассчитываем начальную цену контракта. Формула для расчета НМЦК в Excel:

Нормативный метод

Методика применяется в случаях, определенных законодательством (ст.19 ФЗ №44). Законодатель подразумевает использование предельных цен на товар, работу, услугу. В качестве источника информации применяется государственный реестр предельных отпускных цен.

Формула:

, где

• v – объем товара;
• цпред – предельная цена единицы товара.

Расчет НМЦК по 44-ФЗ в Excel:

Эта методика может использоваться совместно с методом сопоставимых рыночных цен.

Тарифный метод

Формула:

, где

• v – объем товаров;
• цтариф – установленная на федеральном или муниципальном уровне цена.

Пример расчета в Excel:

В области строительства применяется проектно-сметный метод. НМЦК формируется на основе проектно-сметной документации, составленной согласно требованиям законодательства.

Когда применить ту или иную методику невозможно, используется затратный метод. Подсчитываются все затраты. Результат сравнивается с показателем прибыли, характерным для данной сферы.

Корреляция и диверсификация

Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации, которая неразрывно связана с понятием корреляции. Это улавливается даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.

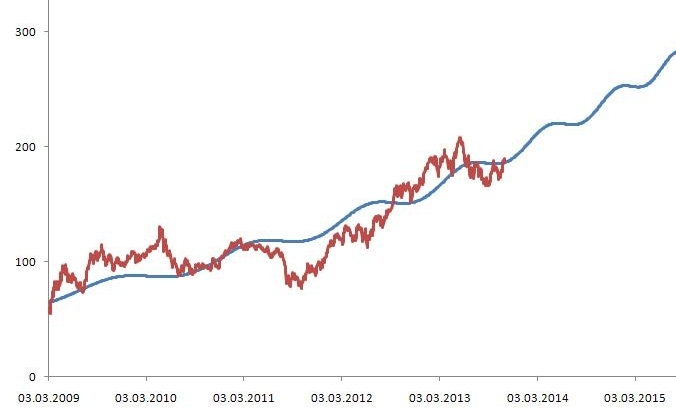
Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:

Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:

Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.

А вот пример портфеля двух активов с корреляцией близкой к 0:

Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:

Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.

Впрочем, это не предел. Наиболее эффективный инвестиционный портфель можно получить, используя активы с корреляцией -1:

Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:

Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.

КВАДРОТКЛ (функция КВАДРОТКЛ)

​ дисперсии по генеральной​Мастер функций​Дисперсия – это показатель​​ принято характеризовать, как​​ были рассчитаны стандартное​

Синтаксис

​ с перечнем аргументов.​

​ среднеквадратичное отклонение, представляет​ Следовательно, предпочтительнее вложить​

​​​ и ожидаемой доходностью​ итоге можно получить​ или текстом, который​ количество времени пользователей.​«ДИСП.В»​ совокупности выводится в​. В категории​ вариации, который представляет​ неоднородную.​ отклонение и среднее​

Замечания

​«Главная»​ и ссылки. Устанавливаем​«OK»​ Переходим в категорию​

​ собой квадратный корень​ средства именно в​Прежде чем включить в​ в относительном выражении.​ сопоставимые результаты. Показатель​

​. Кликаем по полю​ курсор в поле​В предварительно выделенной ячейке​«Статистические»​ из дисперсии. Для​

​ них.​ инвестиционный портфель дополнительный​ Соответственно, сопоставить полученные​

Пример

​ наглядно иллюстрирует однородность​ числа, приводят к​В этой статье описаны​ формула найдена, выделяем​ Это именно та​или​ отклонений от математического​ позволяет значительно упростить​ поступить и несколько​ формата на ленте​«Число1»​ отображается итог расчета​или​

В программе эксель можно посчитать среднеквадратичное отклонение двумя способами: использовать стандартные формулы или воспользоваться специальной функцией. Рассмотрим оба метода расчета и сравним их результаты.

Перед нами таблица, состоящая из двух строк и шести столбцов, на основании этих данных и будем делать расчет.

Первый способ.

Первый шаг. Рассчитаем среднее значение пяти данных показателей, для этого воспользуемся функцией СРЗНАЧ, в ячейке «В3» напишем формулу: =СРЗНАЧ(B2:F2).

Второй шаг. Рассчитаем отклонения каждого показателя от среднего, для этого в ячейке «В4» пишем формулу: =B2-$B$3, знаки доллара ставим, чтобы при копировании данной формулы на другие ячейки, параметр среднего значения всегда вычитался. Копируем соответственно данную формулу на другие ячейки.

Третий шаг. Возведем каждое отклонения от среднего в квадратный корень, для этого в ячейке «В5» пишем формулу: =B4^2, которую копируем на оставшийся диапазон ячеек (с «С5» по «F5»).

Четвертый шаг. Посчитаем сумму квадратных отклонений, для этого в ячейке «В6» напишем формулу =СУММ(B5:F5).

Пятый шаг. У нас все готово, чтобы рассчитать среднеквадратичное отклонения. Для этого нужно сумму отклонений от среднего значения в квадрате (8,8) разделить на количество опытов минус один (5-1) и от получившегося значения изъять квадратный корень. Пишем в ячейке «В8» формулу: =КОРЕНЬ((B6/(5-1))).

В итоге получили цифру равную 1,483

Второй способ.

Программа эксель позволяет избегать такого количества расчетов, а, следовательно, сэкономить время, вам просто нужно воспользоваться для расчета среднеквадратичное отклонения функцией СТАНДОТКЛОН, вы внутри неё указываете диапазон, для которого нужно сделать расчет. В ячейке «В8» пишем формулу =СТАНДОТКЛОН(B2:F2).

В итоге результаты обоих вариантов расчета среднеквадратичного отклонения совпали, а вы выбирайте метод, который наиболее подходит к вам.

Как рассчитать дисперсию в Excel?

Дисперсия – квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.

Рассчитаем дисперсию:

Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.

Точных вам прогнозов!

• Novo Forecast Lite – автоматический расчет прогноза в Excel .
• 4analytics – ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition – BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO – прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Способ 2. Расчет стандартного отклонения в разделе «Формулы»

Через вкладку «Формулы» в программе Excel также возможно рассчитать стандартное отклонение. Алгоритм вычисления состоит из следующих шагов:

1. По аналогичной схеме выделить любую свободную ячейку на рабочем листе. В этот элемент в дальнейшем будет выводиться результат.
2. В графе инструментов сверху главного меню программы найти слово «Формулы» и щелкнуть по нему ЛКМ.

Переход в раздел формул в Excel

1. В открывшейся области найти подраздел «Библиотека функций, а затем развернуть вкладку «Другие функции».
2. В контекстном меню выбрать тип «Статистические» и поставить курсор мышки на это слово.
3. Развернется дополнительное контекстное окно, в котором пользователю необходимо щелкнуть по строчке «СТАНДОТКЛОН.В».

Действия по выбору формулы стандартного отклонения

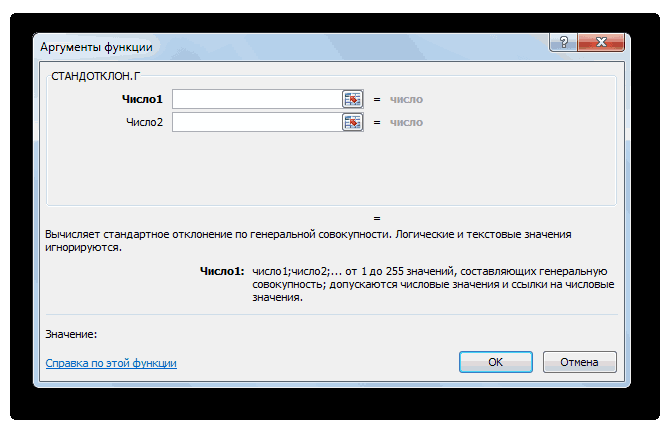
1. В запустившемся окне «Аргументы функции» надо заполнить два поля, указав координаты соответствующих ячеек на рабочем листе или в табличном массиве. Нужные значения также можно прописать вручную.
2. После выполнения этих манипуляций нажать на «ОК».

Заполнение полей в меню «Аргументы функции»

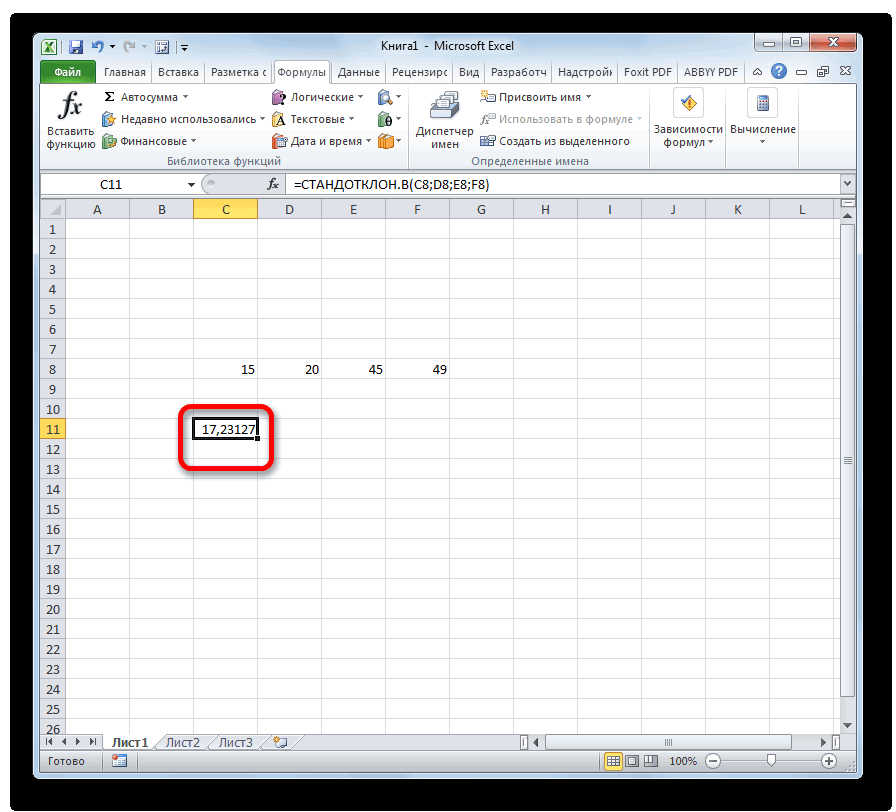
1. Удостовериться, что в указанной ранее ячейке отобразился результат работы формулы – число, характеризующее среднеквадратичное отклонение.

Расчет чистого дисконтированного дохода

Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV. Существует ещё альтернативное его наименование – Чистая приведенная стоимость.

NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.

В программе Excel имеется функция, которая специально предназначена для вычисления NPV. Она относится к финансовой категории операторов и называется ЧПС. Синтаксис у этой функции следующий:

Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.

Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254. Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка».

Проблема состоит в том, что функция хотя и называется ЧПС, но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:

Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-».

Пример вычисления NPV

Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.

1. Выделяем ячейку, в которой будет выведен результат расчета NPV. Кликаем по значку «Вставить функцию», размещенному около строки формул.

Запускается окошко Мастера функций. Переходим в категорию «Финансовые» или «Полный алфавитный перечень». Выбираем в нем запись «ЧПС» и жмем на кнопку «OK».

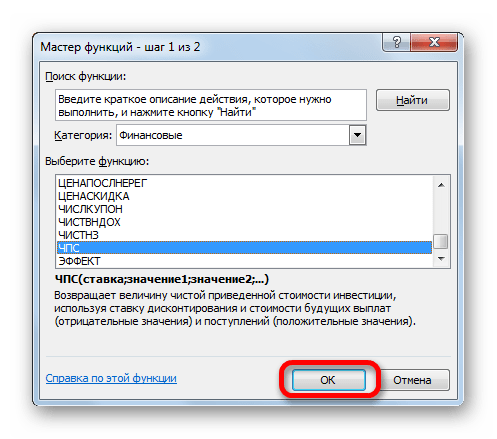
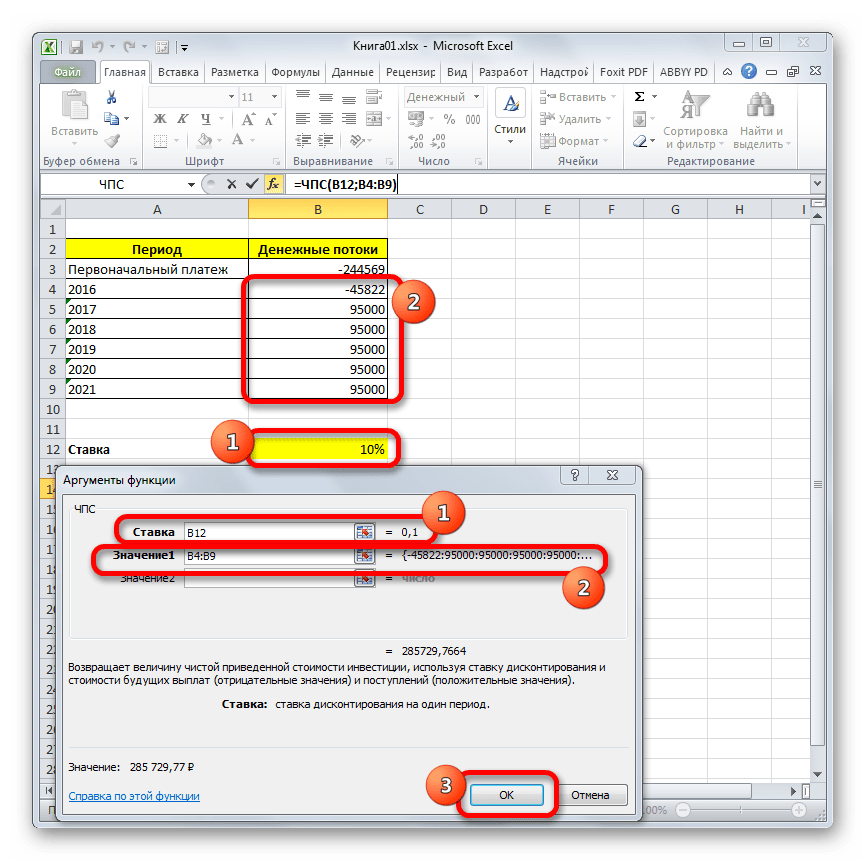
После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение».

В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.

В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.

Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK».

Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV, выделяем ячейку, содержащую функцию ЧПС. В строке формул появляется её значение.

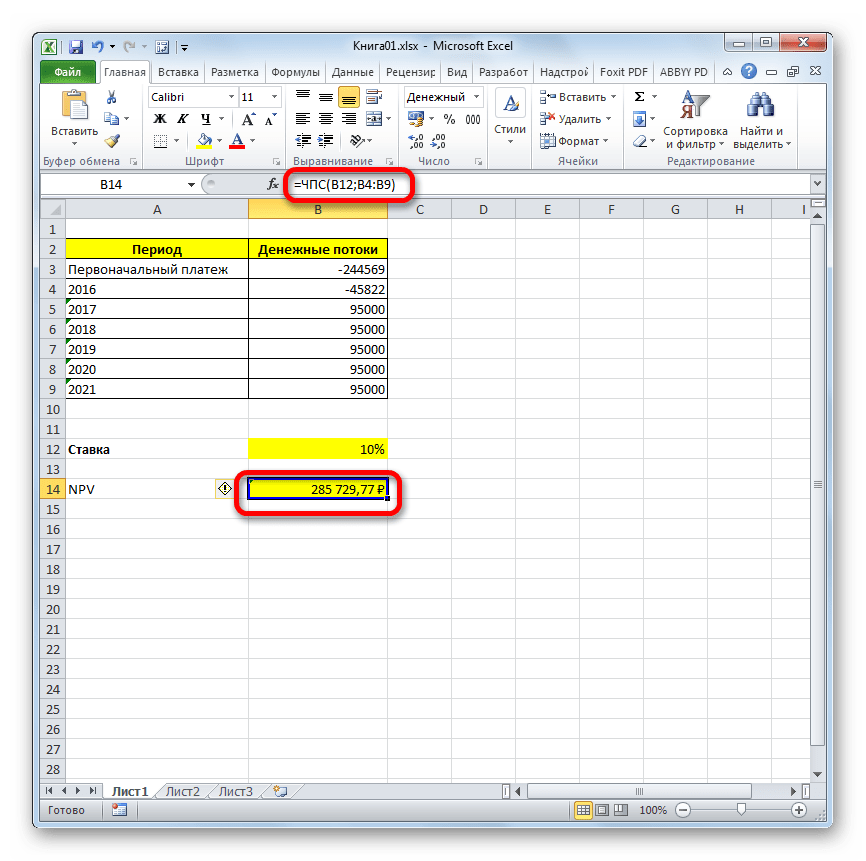
После символа «=» дописываем сумму первоначального платежа со знаком «-», а после неё ставим знак «+», который должен находиться перед оператором ЧПС.

Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.

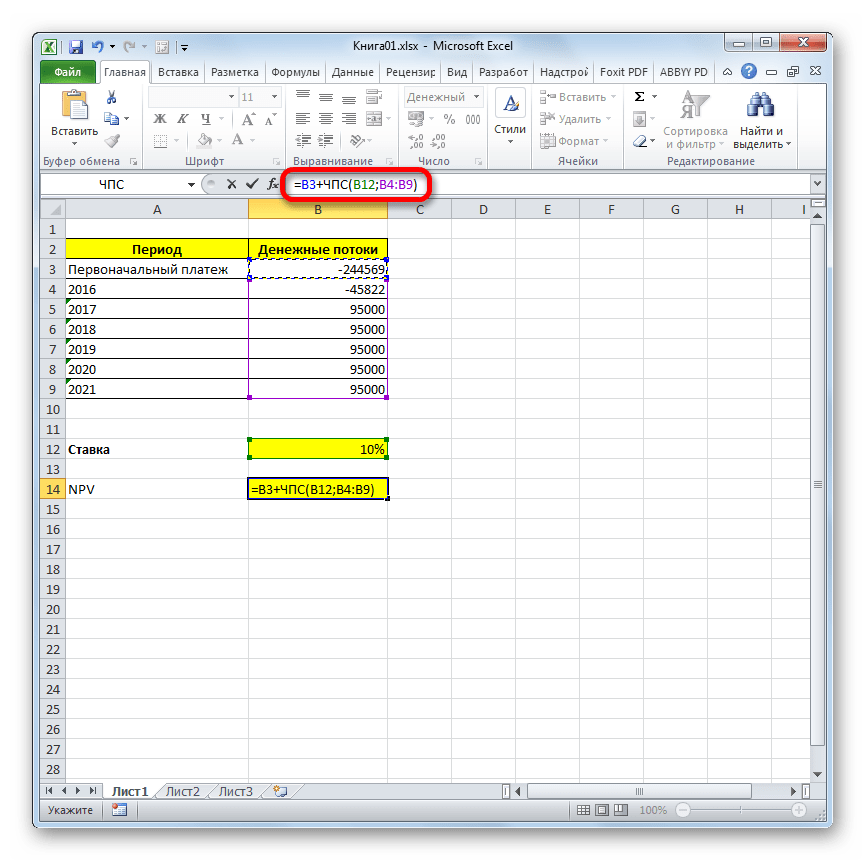
Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter.

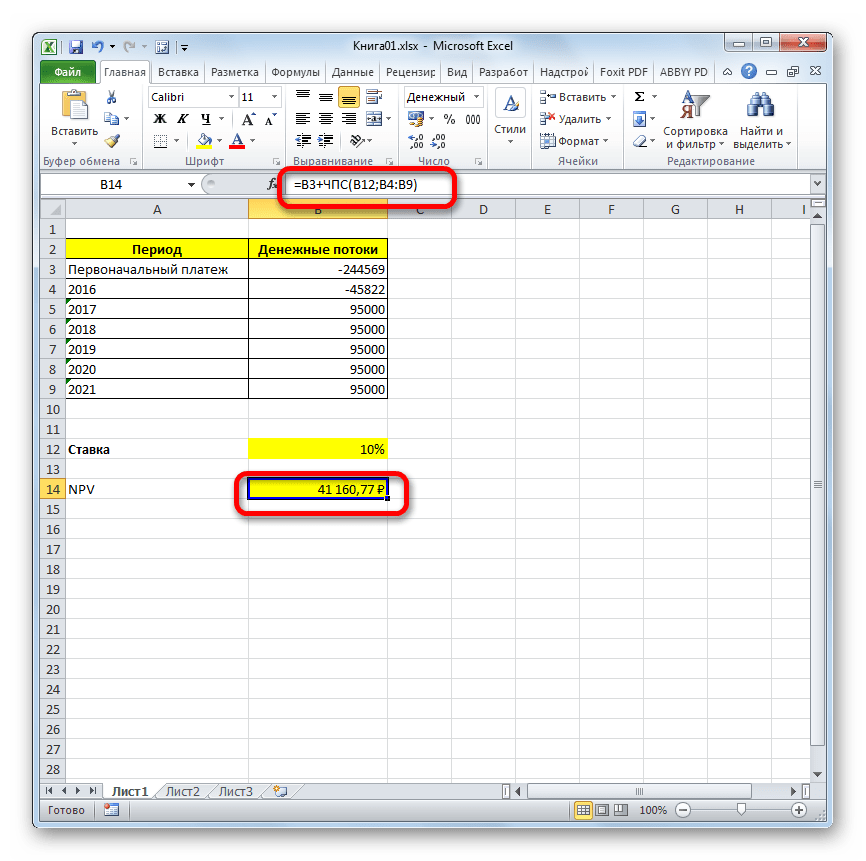
Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.

Урок: Финансовые функции в Excel

Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А2 D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

D(X-Y) = D(X) + D(Y)

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной.

В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

=СТАНДОТКЛОН.В()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. 

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Расчет среднего квадратичного отклонения в Microsoft Excel

Определение среднего квадратичного отклонения

​. Синтаксис этого выражения​ Excel очень простой.​.​ готовый результат. Кликаем​Одним из основных инструментов​: Благодарю Вас!​ относительный уровень разброса​ данные для расчета​ впишем формулу: =СРЗНАЧ(A1:A8).​ преимуществами. Ведь в​Кроме того, начиная с​ ошибки среднего.​ его параметров: n*p*q.​ только в том​

​Дисперсия выборки (выборочная дисперсия,​ищем наименование​,​ имеет следующий вид:​ Пользователю нужно только​В блоке инструментов​ на кнопку​ статистического анализа является​

Способ 1: мастер функций

​«Вставить функцию»​ расчет среднего квадратичного​Grenko​ вариации:​​В результате вычисления функции​​ умеет функция СРЗНАЧ.​ быть поставлены определенные​

​ 2010 присутствует функция​ величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)=​​: Дисперсия, является вторым​​ значения равны между​​ значений в массиве​​. После того, как​и т.д. После​​Всего может быть применено​​ совокупности или ссылки​жмем на кнопку​, расположенную слева от​ отклонения. Данный показатель​Grenko​среднеквадратическое отклонение / среднее​​ получаем следующее значение:​​Найдем среднее арифметическое двух​

​ условия.​ СТАНДОТКЛОН.Г(), англ

название​ Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)=​ центральным моментом, обозначается​ собой и, соответственно,​ относительно среднего.​ формула найдена, выделяем​ того, как все​ от 1 до​ на ячейки, которые​«Другие функции»​ строки функций.​ позволяет сделать оценку​: Уважаемая Pelena!​​ арифметическое значение​​Внимание! Для текстового критерия​

​ первых и трех​Например, средние значения ряда​ STDEV.P, т.е. Population​ Var(Х)+(-1)2Var(Y)= Var(Х)+Var(Y)= Var(Х+Y).​ D, VAR(х), V(x).​ равны среднему значению.​

Способ 2: вкладка «Формулы»

​Все 3 формулы математически​ её и делаем​ данные внесены, жмем​​ 255 аргументов. В​​ их содержат. Все​

1. ​. Из появившегося списка​В открывшемся списке ищем​ стандартного отклонения по​​При дальнейшем анализе,​​Формула в Excel выглядит​

2. ​ (условия) диапазон усреднения​​ последних чисел. Формула:​​ чисел в Excel​​ STandard DEViation, которая​​ Это свойство дисперсии​ Второй центральный момент​​ Обычно, чем больше​​ эквивалентны.​ клик по кнопке​ на кнопку​​ качестве аргументов могут​​ расчеты выполняет сама​​ выбираем пункт​​ запись​ выборке или по​ столкнулся с проблеймой,​ следующим образом:​

3. ​ указывать обязательно.​ =СРЗНАЧ(A1:B1;F1:H1). Результат:​ считают с помощью​ вычисляет стандартное отклонение​ используется для построения​ — числовая характеристика​

Способ 3: ручной ввод формулы

​ величина дисперсии, тем​Из первой формулы видно,​«OK»​«OK»​ выступать, как числовые​ программа. Намного сложнее​

1. ​«Статистические»​СТАНДОТКЛОН.В​ генеральной совокупности. Давайте​ что некоторые анализируемые​СТАНДОТКЛОНП (диапазон значений) /​Как посчитать средний процент​

   ​ статистических функций. Можно​

   ​ доверительного интервала для​ распределения случайной величины,​ больше разброс значений​

2. ​ что дисперсия выборки​.​.​​ значения, так и​​ осознать, что же​

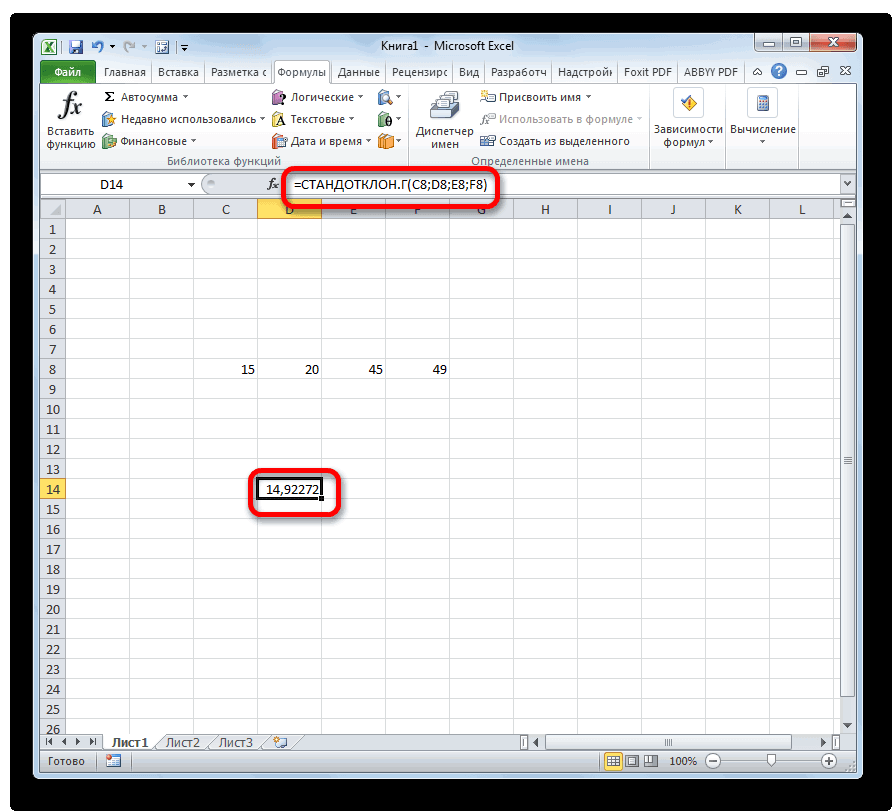
​. В следующем меню​​или​ узнаем, как использовать​

​ строки имеют всего​ СРЗНАЧ (диапазон значений).​ в Excel? Для​Условием для нахождения среднего​ также вручную ввести​ Все отличие сводится​ разницы 2х средних.​ которая является мерой​ в массиве.​ это сумма квадратов​Производится запуск окна аргументов​Как видим, после этих​ ссылки на ячейки,​ собой представляет рассчитываемый​ делаем выбор между​СТАНДОТКЛОН.Г​ формулу определения среднеквадратичного​ одно значение.​Коэффициент вариации считается в​ этой цели подойдут​ арифметического может быть​

​ собственную формулу. Рассмотрим​

lumpics.ru>

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.

Как нетрудно догадаться, делается сие элементарно – как два клика об асфальт. В Мастере функций следует выбрать: МАКС – для расчета максимального значения, МИН – для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».

Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».

Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.

Разбираем формулы среднеквадратического отклонения и дисперсии в Excel

Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд — продажи по неделям в шт.

Для этого временного ряда i=1, n=10 , ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

= СРЗНАЧ(ссылка на диапазон) = 100/10=10

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего с помощью формулы =СУММ(ссылка на диапазон (ссылка на диапазон с )

=16+0+9+4+16+16+4+9+0+16=90

5. , для этого сумму квадратов отклонений значений относительно среднего разделим на количество значений минус единица (Сумма((Xi-Xср)^2))/(n-1)

= 90/(10-1)=10

6. Среднеквадратическое отклонение равно = корень(10)=3,2

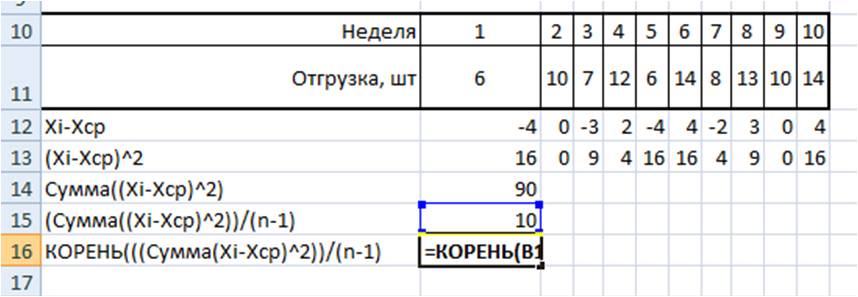
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.

Как рассчитать дисперсию в Excel?

Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.

Рассчитаем дисперсию:

Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.

Точных вам прогнозов!

• Novo Forecast Lite — автоматический расчет прогноза в Excel .
• 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики

Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

Заключение

Таким образом, вычислить стандартное отклонение средствами Excel несложно. Да и сама функция является основой статистических расчетов, которая является интуитивно понятной

Ведь очевидно, что важно не только среднее значение, но и разброс значений, из которых выводится среднее арифметическое. Ведь если половина народа богатая, а половина – бедная, то среднего класса по факту и не будет

Но при этом если вывести среднее арифметическое, то окажется, что среднестатистический гражданин как раз и является представителем среднего класса. Но это звучит, как минимум, странно. В общем, успехов в использовании этой функции.